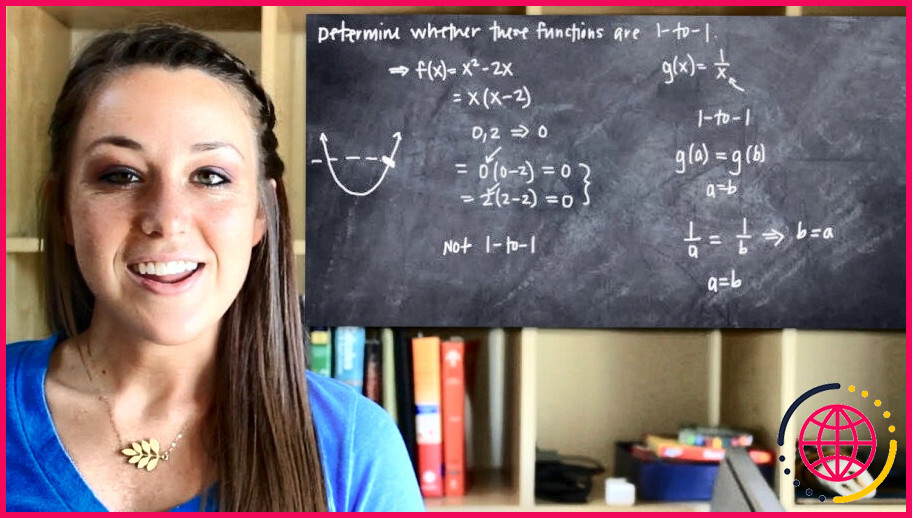Comment déterminer si une fonction est une fonction biunivoque ?

Un moyen facile de déterminer si une fonction est une fonction de un à un est d’utiliser le test de la ligne horizontale sur le graphique de la fonction . Pour ce faire, il faut tracer des lignes horizontales à travers le graphique. Si toute ligne horizontale intersecte le graphique plus d’une fois, alors le graphique ne représente pas une fonction biunivoque .

Simplement, qu’est-ce qu’un exemple de fonction biunivoque ?

Une fonction biunivoque est une fonction dont les réponses ne se répètent jamais. Pour exemple , la fonction f(x) = x + 1 est une fonction biunivoque car elle produit une réponse différente pour chaque entrée. Une façon simple de tester si une fonction est une-à-une ou non est d’appliquer le test de la ligne horizontale à son graphique.

On peut aussi se demander comment on peut savoir si une fonction est paire ou impaire. Test pour déterminer si une fonction y=f(x) est paire , impaire ou ni l’un ni l’autre : Remplacer x par -x et comparer le résultat à f(x). Si f(-x) = f(x), la fonction est paire . Si f(-x) = – f(x), la fonction est odd .

Alors, comment écrire une fonction biunivoque ?

Une fonction pour laquelle chaque élément de l’étendue de la fonction correspond exactement à un élément du domaine. Une à une est souvent écrite 1-1. Remarque : y = f(x) est une fonction si elle passe le test de la ligne verticale. C’est une fonction 1-1 si elle passe à la fois le test de la ligne verticale et le test de la ligne horizontale.

Est-ce que many to one est une fonction ?

Une fonction est dite one -to- one si chaque valeur y a exactement une valeur x qui lui est affectée, et many-to-one s’il y a des valeurs y qui ont plus de une valeur x qui leur est affectée. Ce graphique montre une fonction many-to-one . Les trois points indiquent trois valeurs x qui sont toutes mises en correspondance avec la même valeur y.

Les paraboles sont-elles des fonctions biunivoques ?

La fonction f(x)=x² n’est pas ponctuelle car f(2) = f(-2). Son graphe est une parabole , et de nombreuses lignes horizontales coupent deux fois la parabole . La fonction f(x)=x 3, par contre, EST univoque . Si deux nombres réels ont le même cube, ils sont égaux.

Comment vérifier si une équation est une fonction ?

Il est relativement facile de déterminer si une équation est une fonction en résolvant y. Lorsque on vous donne une équation et une valeur spécifique pour x, il ne devrait y avoir qu’une seule valeur de y correspondante pour cette valeur de x. Par exemple, y = x + 1 est une fonction parce que y sera toujours supérieur de un à x.

Qu’est-ce qu’une fonction paire ?

DÉFINITION. Une fonction f est paire si le graphe de f est symétrique par rapport à l’axe des y. Algébriquement, f est pair si et seulement si f(-x) = f(x) pour tout x dans le domaine de f. Une fonction f est odd si le graphique de f est symétrique par rapport à l’origine.

.
Que signifie « injectif » ?

En mathématiques, une fonction injective (aussi appelée injection, ou fonction biunivoque) est une fonction qui fait correspondre des éléments distincts de son domaine à des éléments distincts de son codomaine. En d’autres termes, chaque élément du codomaine de la fonction est l’image d’au plus un élément de son domaine.

Qu’est-ce qu’une fonction en mathématiques ?

En mathématiques, une fonction est une relation entre ensembles qui associe à tout élément d’un premier ensemble exactement un élément du second ensemble. Le symbole qui est utilisé pour représenter l’entrée est la variable de la fonction (on dit souvent que f est une fonction de la variable x)

.
Qu’est-ce qui fait qu’une fonction n’est pas univoque ?

Si une certaine ligne horizontale coupe le graphe de la fonction plus d’une fois, alors la fonction est non univoque . Si aucune ligne horizontale ne coupe le graphe de la fonction plus d’une fois, alors la fonction est unique .

Qu’est-ce qui n’est pas une fonction ?

Fonctions . Une fonction est une relation dans laquelle chaque entrée n’a qu’une seule sortie. Dans la relation , y est une fonction de x, car pour chaque entrée x (1, 2, 3 ou 0), il n’y a qu’une seule sortie y. x est non fonction de y, car l’entrée y = 3 a plusieurs sorties : x = 1 et x = 2.

Quels types de fonctions sont un à un ?

Types de fonctions :

• Fonction un à un(Injective) : Une fonction est dite un à un si pour tous les éléments a et b dans A, si f(a) = f(b),alors il doit être le cas que a = b.
• Fonction Onto (surjective) : Si tout élément b dans B a un élément correspondant a dans A tel que f(a) = b.

Qu’est-ce qui rend une fonction onto ?

En mathématiques, une fonction f d’un ensemble X vers un ensemble Y est surjective (on dit aussi surto , ou une surjection), si pour tout élément y dans le codomaine Y de f, il existe au moins un élément x dans le domaine X de f tel que f(x) = y.

Qu’est-ce qui fait d’une relation une fonction ?

Une relation d’un ensemble X à un ensemble Y est appelée une fonction si chaque élément de X est relié à exactement un élément de Y, c’est-à-dire que, étant donné un élément x dans X, il n’y a qu’un seul élément dans Y auquel x est relié. C’est une fonction puisque chaque élément de X est relié à un seul élément de Y.

Quel est l’exemple d’une fonction ?

Quelques Exemples de Fonctions x² (élévation au carré) est une fonction . x³+1 est aussi une fonction . Sinus, Cosinus et Tangente sont des fonctions utilisées en trigonométrie. et il y en a beaucoup d’autres!

Comment savoir si c’est une fonction ou non ?

Le test de la ligne horizontale La valeur x d’un point où une ligne verticale intersecte une fonction représente l’entrée pour cette valeur y de sortie. Si nous pouvons tracer n’importe quelle ligne horizontale qui intersecte un graphique plus d’une fois, alors le graphique ne pas représente une fonction car cette valeur y a plus d’une entrée.

Une ligne horizontale est-elle une fonction univoque ?

Si une ligne horizontale intersecte plus d’une fois le graphe d’une fonction , alors la fonction n’est pas univoque . Remarque : La fonction y = f(x) est une fonction si elle passe le test de la ligne verticale. C’est une fonction biunivoque si elle passe à la fois le test de la ligne verticale et celui de la ligne horizontale.

Quelles sont les caractéristiques d’une fonction exponentielle ?

Les graphes des fonctions de la forme y = b^x ont certaines caractéristiques en commun. Les fonctions exponentielles sont des fonctions univoques. Le graphique passe le test de la ligne horizontale pour fonctionnelle inverse. Le graphique est asymptotique par rapport à l’axe des x – se rapproche très, très près de l’axe des x mais, dans ce cas, ne le touche pas ou ne le traverse pas.

Quel est l’exemple d’une fonction impaire ?

On les a appelées ‘ odd ‘ parce que les fonctions x, x³, x⁵, x⁷, etc se comportent comme ça, mais il y a d’autres fonctions qui se comportent comme ça aussi, comme sin(x) : Sinus fonction : f(x) = sin(x) C’est une fonction odd . Mais un exposant odd ne fait pas toujours une fonction odd , par exemple x³+1 n’est pas une fonctionodd .

Qu’est-ce qu’une fonction par morceaux en mathématiques ?

En mathématiques , une fonction définie par morceaux (aussi appelée fonction par morceaux ou fonction hybride) est une fonction qui est définie par de multiples sous- fonctions , chaque sous- fonction s’appliquant à un certain intervalle du domaine de la fonction principale (un sous-domaine).

Une fonction linéaire est-elle paire ou impaire ?

Il est important de se rappeler qu’une fonction ne doit pas nécessairement être paire ou impaire . La plupart des fonctions ne sont ni paires ni impaires . Pour déterminer si la fonction eginalign*y=3(x+2)^2+4endalign* est paire ou impaire , appliquez le test des deux types.