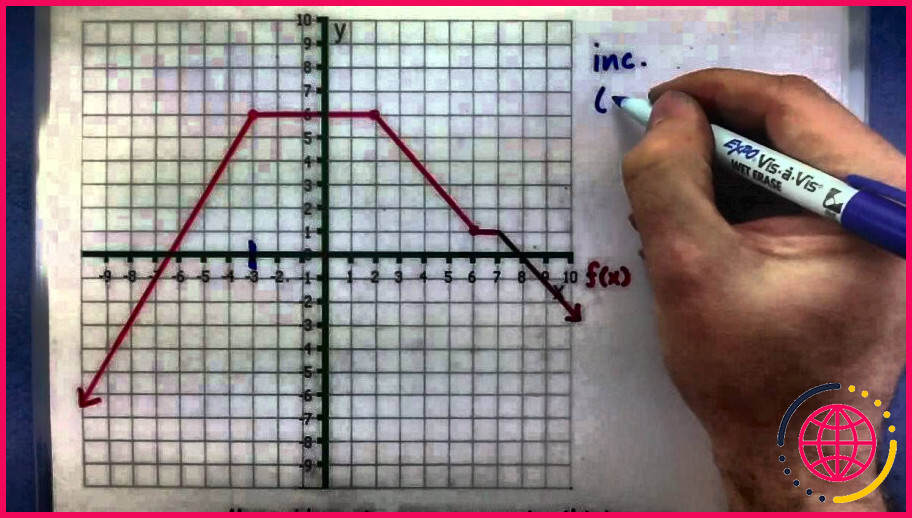
Comment savoir si une fonction est croissante décroissante ou constante ?

Si f′(x) &gt ; 0, alors f est croissante sur l’intervalle, et si f′(x) &lt ; 0, alors f est décroissante sur l’intervalle. Cette information et d’autres peuvent être utilisées pour montrer une esquisse raisonnablement précise du graphique de la fonction . Exemple 1 : Pour f(x) = x ⁴ – 8 x ² déterminez tous les intervalles où f est croissante ou décroissante .

Par ailleurs, comment savoir si une fonction est constante ?

Pour cette raison, une fonction constante a la forme y = b, où b est une constante (une valeur unique qui ne change pas). Par exemple, y = 7 ou y = 1 094 sont des fonctions constantes . Quelle que soit l’entrée, ou la valeur x, la sortie, ou la valeur y, est toujours la même.

En outre, qu’est-ce qui rend une fonction constante ? En mathématiques, une fonction constante est une fonction dont la valeur (de sortie) est la même pour chaque valeur d’entrée. Par exemple, la fonction est une fonction constante car la valeur de est 4 quelle que soit la valeur d’entrée. (voir image).

Les gens se demandent également ce que cela signifie quand une fonction est décroissante ?

Le graphique a une pente positive. Par définition : Une fonction est strictement croissante sur un intervalle, si lorsque x₁ &lt ; x₂, alors f (x₁) &lt ; f (x₂). Décroissante : Une fonction est décroissante , si lorsque x augmente (lecture de gauche à droite), y diminue.

Une fonction peut-elle être croissante et négative en même temps ?

Incroissance , décroissance, intervalles positifs ou négatifs . Les valeurs des fonctions peuvent être positives ou négatives , et elles peuvent augmenter ou diminuer lorsque l’entrée augmente.

Comment trouve-t-on un intervalle ?

Conclusion

1. Un intervalle est l’ensemble des nombres compris entre deux nombres donnés.
2. Montrer si le nombre de début et de fin sont inclus est important.
3. Il existe trois principales façons de montrer les intervalles : Les inégalités, la ligne de nombres et la notation de l’intervalle.

Le domaine est-il toujours constitué de tous les nombres réels ?

Le domaine est tous les nombres réels sauf 0. Comme la division par 0 est indéfinie, (x-3) ne peut pas être 0, et x ne peut pas être 3. Domaine est tous les nombres réels sauf 3. Puisque la racine carrée de tout nombre inférieur à 0 est indéfinie, (x+5) doit être égal ou supérieur à zéro.

Qu’est-ce qu’une fonction par morceaux en mathématiques ?

En mathématiques , une fonction définie par morceaux (aussi appelée fonction par morceaux ou fonction hybride) est une fonction qui est définie par plusieurs sous- fonctions , chaque sous- fonction s’appliquant à un certain intervalle du domaine de la fonction principale (un sous-domaine).

Une fonction constante est-elle sur ?

Une fonction constante y = C, C constante ne peut JAMAIS être biunivoque puisque pour différentes valeurs de x on a la même valeur de y, à savoir C. Par contre toute fonction constante y = C EST ponctuelle puisque pour chaque valeur de y, en l’occurrence y = C, on peut trouver au moins un x tel que f(x) = C.

Quel est l’exemple de constante ?

Constante . plus Une valeur fixe. En algèbre, une constante est un nombre à part entière, ou parfois une lettre comme a, b ou c pour représenter un nombre fixe. Exemple : dans « x + 5 = 9 », 5 et 9 sont des constantes.

Qu’est-ce qu’une fonction non linéaire ?

Algébriquement, les fonctions linéaires sont des polynômes dont l’exposant le plus élevé est égal à 1 ou de la forme y = c où c est une constante. Les fonctions non linéaires sont toutes les autres fonctions . Un exemple de fonction non linéaire est y = x^2. Elle est non linéaire car, bien qu’il s’agisse d’un polynôme, son exposant le plus élevé est 2, et non 1.

Qu’est-ce qu’une fonction constante sur un graphique ?

Une fonction constante est une fonction dont la plage est constituée d’un seul élément. C’est-à-dire que la valeur de sortie de la fonction à toute valeur d’entrée dans son domaine est la même, indépendamment de l’entrée. Le graphique d’une fonction constante est une ligne horizontale, c’est-à-dire une ligne de pente 0.

Une fonction biunivoque doit-elle être continue ?

Si elle ne coupe le graphe qu’en un point, alors la fonction est un – un . Alternativement, une fonction est une une – une fonction , si f(x) est une fonction continue et est soit croissante soit décroissante dans le domaine donné.

Quelle est l’étendue d’une constante ?

Une fonction constante est une fonction linéaire pour laquelle la plage .
ne change pas quel que soit le membre du domaine utilisé. f(x1)=f(x2) pour tout x1 et x2 dans le domaine. Avec une fonction constante , pour deux points quelconques de l’intervalle, une variation de x entraîne une variation nulle de f(x) .

Qu’est-ce qu’une fonction paire ?

DÉFINITION. Une fonction f est paire si le graphe de f est symétrique par rapport à l’axe des y. Algébriquement, f est pair si et seulement si f(-x) = f(x) pour tout x dans le domaine de f. Une fonction f est odd si le graphique de f est symétrique par rapport à l’origine.

Qu’est-ce qu’une fonction mère en mathématiques ?

En mathématiques , une fonction parente est la fonction la plus simple d’une famille de fonctions qui préserve la définition (ou la forme) de toute la famille. Par exemple, pour la famille des fonctions quadratiques ayant la forme générale. la fonction la plus simple est .

.
Que signifie le fait qu’une fonction soit croissante ou décroissante ?

Fonctions croissantes et décroissantes . Définition des fonctions incrémentales et décrémentales . Nous savons tous que si quelque chose est incroissant alors il monte et si il est décroissant il descend. Une autre façon de dire qu’un graphique va vers le haut est que sa pente est positive. Si le graphique descend, alors la pente serait

.
Une fonction décroissante implique-t-elle qu’elle est négative ?

Une dérivée positive signifie que la fonction est croissante. Une dérivée négative signifie que la fonction est décroissante . Une dérivée nulle signifie que la fonction a un comportement particulier au point donné. Elle peut avoir un maximum local, un minimum local, (ou dans certains cas, comme nous le verrons plus tard, un point de « retournement »)

.
Comment montrer qu’une fonction est strictement décroissante ?

Disons que votre fonction est f(x). Trouvez ensuite f'(x). Si f'(x) &gt ; 0 pour toutes les valeurs de x, alors elle est strictement croissante. Si f'(x) &lt ; 0 pour toutes les valeurs de x, alors elle est strictement décroissante .

Que vous dit la dérivée seconde ?

La dérivée seconde nous dit beaucoup de choses sur le comportement qualitatif du graphique. Si la dérivée seconde est positive en un point, le graphique est concave vers le haut. Si la dérivée seconde est positive en un point critique, alors le point critique est un minimum local. La dérivée seconde sera nulle à un point d’inflexion.

Quelle section de la fonction est décroissante ?

Informellement . Une fonction est croissante sur une section si le graphique de cette section « monte » vers la droite. Une fonction est décroissante sur une section si le graphique de cette section ‘tombe’ vers la droite.

Une parabole est-elle croissante ou décroissante ?

En parcourant la courbe de la parabole de gauche à droite, si les valeurs des y sont incroissantes , alors elle est incroissante . En allant de gauche à droite, si les valeurs des y sont de plus en plus petites, alors elle est décroissante . Si la parabole s’ouvre, le graphique sera décroissant jusqu’à ce que vous arriviez au sommet.