La négation est-elle une connective logique ?

La négation est un connecteur logique, un mot utilisé pour joindre deux phrases ou clauses ensemble afin de former une déclaration négative. Le connecteur de négation le plus courant est le mot « pas ». D’autres connecteurs de négation incluent « non », « jamais » et « aucun ».

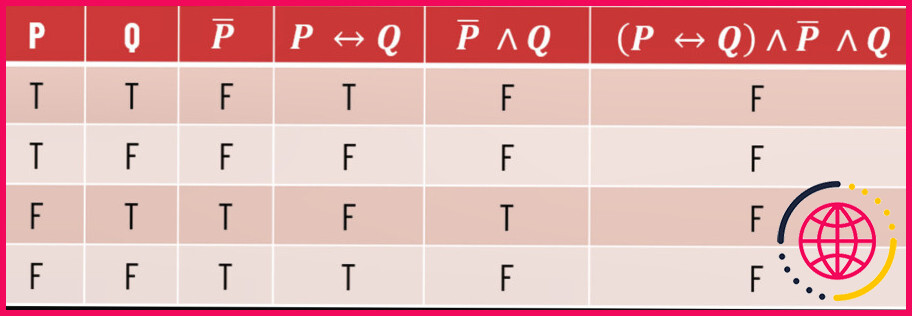
La négation est un concept fondamental en logique et en mathématiques. Dans les systèmes formels de logique, tels que la logique propositionnelle et la logique des prédicats, les valeurs de vérité des énoncés composés sont déterminées par les valeurs de vérité de leurs composants et les connecteurs entre eux. Par exemple, dans la logique propositionnelle, l’énoncé « P ∧ Q » (lu comme « P et Q ») est vrai si P et Q sont vrais ; si P ou Q est faux, alors « P ∧ Q » est faux. L’énoncé « ¬P ∧ Q » (lu comme « non-P et Q ») est vrai si P est faux et Q est vrai ; si P ou Q est faux, alors « ¬P ∧ Q » est faux.

En mathématiques, le concept de négation est souvent exprimé en termes d’opérations ensemblistes. Par exemple, étant donné un ensemble A, la négation de A (écrite comme A′) est l’ensemble de tous les éléments qui ne sont pas dans A. Donc si A = {1, 2, 3}, alors A′ = {4, 5 , 6}. De même, étant donné une proposition P(x), la négation de P(x) (écrite ¬P(x)) est la proposition que P(x) n’est pas vraie ; c’est-à-dire ¬P(x) = {x : P(x) est faux}.

Les connecteurs communs comprennent la négation, la disjonction, la conjonction et l’implication. Une connective logique est similaire, mais pas équivalente, à une syntaxe couramment utilisée dans les langages de programmation appelée opérateur conditionnel.

Quelles sont les cinq connectives logiques de base ?

Les cinq (5) connecteurs ou opérateurs logiques courants.

• La négation logique.
• Conjonction logique (ET)
• Disjonction logique (OU inclusif).
• Implication logique (conditionnel)
• Biconditionnel logique (Double Implication)

La négation est-elle une conjonctive ?

Les conjonctives couramment utilisées comprennent  » mais « ,  » et « ,  » ou « ,  » si .alors  » et  » si et seulement si « . Les différents types de connecteurs logiques comprennent la conjonction ( » et « ), la disjonction ( » ou « ), la négation ( » pas « ), le conditionnel ( » si .alors « ) et le biconditionnel ( » si et seulement si « ).

La négation est-elle une connective fonctionnelle de vérité ?

Il existe 5 types de connecteurs fonctionnels de vérité couramment utilisés : Une négation est une proposition affirmant qu’une autre proposition est fausse. Une conjonction est une proposition affirmant que deux autres propositions sont toutes deux vraies. Une disjonction est une proposition affirmant qu’au moins une de deux propositions est vraie.

Quels sont les 5 opérateurs logiques ?

Il existe cinq symboles d’opérateurs logiques : tilde, point, coin, fer à cheval et triple barre.

Quels sont les 3 opérateurs logiques ?

Les opérateurs logiques courants comprennent AND, OR et NOT.

Est-ce que == est un opérateur logique ?

Opérateurs de comparaison – opérateurs qui comparent des valeurs et renvoient vrai ou faux . Les opérateurs comprennent : > , < , >= , <= Opérateurs logiques – opérateurs qui combinent plusieurs expressions ou valeurs booléennes et fournissent une sortie booléenne unique. Les opérateurs comprennent : && , || , et ! .

Est-ce que if/then est fonctionnel à la vérité ?

Une connective logique est fonctionnelle de vérité si la valeur de vérité d’une phrase composée est une fonction de la valeur de vérité de ses sous-sentences. Une classe de connecteurs est fonctionnelle à la vérité si chacun de ses membres l’est.

Est-ce que parce que est fonctionnel à la vérité ?

4 Réponses. C’est parce que ‘parce que’ n’est pas fonctionnel à la vérité. Par exemple, les deux affirmations « L’herbe est verte » et « La neige est blanche » sont toutes deux vraies, mais « L’herbe est verte parce que la neige est blanche » est un argument invalide, et donc, en tant qu’affirmation sur la validité de cet argument, une fausse affirmation.

Quelles sont les trois principales connectives logiques en mathématiques ?

Les connecteurs logiques en mathématiques

• OU (∨)
• AND (∧)
• Négation/ NOT (¬)
• Implication / si-alors (→)
• Si et seulement si (⇔).

Quel conjonctif est utilisé pour la négation ?

Les connecteurs logiques couramment utilisés comprennent : La négation (pas) : ¬ , N (préfixe), ~ Conjonction (et) : ∧ , K (préfixe), & , ∙ Disjonction (ou) : ∨ , A (préfixe)

Quel type de conjonctive est le mais ?

Une conjonction est un type de conjonctif (terme désignant tout mot qui relie des morceaux de texte). Dans ce cas, les conjonctions sont utilisées afin de relier deux parties d’une phrase ensemble. Les conjonctions les plus courantes sont les mots et, mais et ou.

Quel est un exemple de négation ?

Une négation est un refus ou un déni de quelque chose. Si votre ami pense que vous lui devez cinq dollars et que vous dites que ce n’est pas le cas, votre déclaration est une négation. « Je n’ai pas tué le majordome » pourrait être une négation, tout comme « Je ne sais pas où est le trésor ». L’acte de dire l’un de ces énoncés est aussi une négation.

Quels sont les exemples de connecteurs logiques ?

• Temps : après, tant que, dès que, avant, depuis, quand, à chaque fois, jusqu’à ce que.
• Manière : comme (par exemple : fais cela comme ton frère le fait.), .
• Raison : depuis, parce que, comme (ex : Il est parti, car il était tard.), .
• Simultané : pendant que, comme (ex.
• Concessif : bien que, même si, bien que, tandis que.
• Additif : en outre, de plus, en outre.

Comment trouver la principale conjonctive logique ?

Le conjonctif principal d’un énoncé est le conjonctif qui a la plus grande portée. C’est-à-dire que si on décompose la phrase en parties, la connective principale est celle qui relie les plus grandes parties de la phrase. S’il n’y a qu’une seule connective, cette connective est la connective principale.

Qu’est-ce que le mais dans les connecteurs logiques ?

Lors de la traduction des phrases anglaises en forme logique, « but » a généralement la même signification que « and », et la phrase « neither A nor B » est traduite par « not A and not B ».

Qu’est-ce qui n’est pas fonctionnel à la vérité ?

LES CONNECTEURS DE PHRASE NON FONCTIONNELS À LA VÉRITÉ.

Certains mots qui relient des phrases entières ne sont pas fonctionnels à la vérité. C’est-à-dire que le fait de connaître la vérité des parties n’est pas suffisant pour nous permettre de calculer la vérité de l’affirmation composée.

Pourquoi la logique fonctionnelle de vérité est-elle importante ?

Fonction de vérité et énoncés conditionnels

La fonction de vérité peut aussi nous aider à mieux comprendre le fonctionnement apparemment déroutant d’une conditionnelle. Vous vous souvenez que nous avons dit dans la leçon sur les conditionnels qu’un conditionnel n’est faux que si l’antécédent est vrai et le conséquent est faux, sinon il est vrai.

Pourquoi la fonction de vérité est-elle importante pour la logique propositionnelle ?

Il reflète le fait que la logique propositionnelle est fonctionnelle de vérité, ce qui signifie que seules les valeurs de vérité des phrases composantes d’une formule sont pertinentes pour la valeur de vérité de la formule, et que les relations logiques entre les propositions sont déterminées par les relations entre les valeurs de vérité de manière cohérente .

La vérité est-elle un binaire ?

Je dirais que oui, la vérité est binaire : il n’y a pas de degrés de vérité entre 0 et 1. Pour deux raisons, je pense que toute proposition a exactement une des deux valeurs de vérité, vraie ou bien fausse.

Qu’est-ce que l’équivalence vérité-fonctionnelle ?

Les phrases P et Q de SL sont équivalentes du point de vue de la fonction de vérité s’il n’existe aucune affectation de valeurs de vérité sur laquelle P et Q ont des valeurs de vérité différentes (c’est-à-dire si, dans la table de vérité concernée, les colonnes sous P et sous Q sont identiques).

Les quantificateurs sont-ils fonctionnels à la vérité ?

Pour chacun de ces quantificateurs, soulignez toute sa portée (cela inclura le quantificateur lui-même). Tous les quantificateurs, connecteurs ou phrases atomiques qui sont inclus dans cette portée doivent être ignorés. Le résultat est la forme vérité-fonctionnelle de la phrase originale.

N’est pas un opérateur logique ?

L’opérateur logique NOT ( ! ) (complément logique, négation) prend la vérité pour la fausseté et vice versa. Il est généralement utilisé avec des valeurs booléennes (logiques). Lorsqu’il est utilisé avec des valeurs non booléennes, il renvoie false si son opérande unique peut être converti en true ; sinon, il renvoie true .