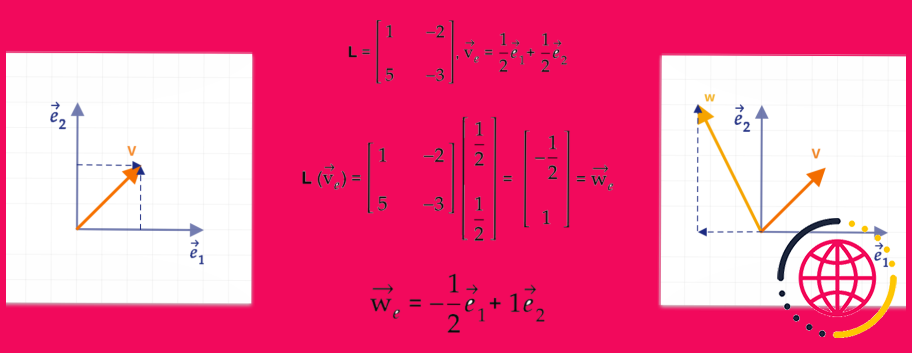Le delta de kronecker est-il un tenseur ?

Le delta de Kronecker, également connu sous le nom de symbole de Kronecker ou fonction de Kronecker, est un tenseur bidimensionnel dont les éléments sont 0 ou 1 et sont donnés par.

delta_{ij} = begin{cases} 1 & text{if } i=j \ 0 & text{if } ineq j. end{cas}.

Le delta de Kronecker peut être utilisé pour exprimer la matrice d’identité :

I=sum_{i}delta_{ij}.

Le delta de Kronecker est étroitement lié au symbole Levi-Civita, qui est un tenseur tridimensionnel. Les deux symboles portent le nom du mathématicien allemand Leopold Kronecker.

Le delta de Kronecker généralisé ou delta de Kronecker multi-index d’ordre 2p est un tenseur de type (p,p) qui est complètement antisymétrique dans ses p indices supérieurs, et aussi dans ses p indices inférieurs.

Le delta de Kronecker est-il une matrice ?

Le delta de Kronecker n’a pas d’éléments. Il ne s’agit pas d’une matrice. C’est une fonction qui prend en entrée la paire (i,j) et renvoie 1 si elles sont identiques et zéro sinon. La matrice identité est une matrice, le delta de Kronecker ne l’est pas.

Le delta de Kronecker est-il une fonction ?

En mathématiques, le delta de Kronecker (du nom de Léopold Kronecker) est une fonction de deux variables, généralement juste des entiers non négatifs. La fonction vaut 1 si les variables sont égales, et 0 sinon : δ i j = { 0 si i ≠ j , 1 si i = j .

Que représente le delta de Kronecker ?

Le symbole porte le nom du mathématicien allemand Leopold Kronecker (1823-1891). L’élément général d’une matrice d’identité peut être écrit comme un delta de Kronecker : les éléments diagonaux (i = j) sont sur…e; les éléments hors diagonale (i ≠ j) sont nuls.

Quel est le rang du tenseur du delta de Kronecker ?

Le tenseur delta de Kronecker de rang est le tenseur de type qui est défini comme suit. Soit le tenseur de type dont les composantes dans tout système de coordonnées sont données par la matrice identité, c’est-à-dire pour tout champ de vecteurs . Alors est obtenu à partir du produit tensoriel -fold de complètement skew-symmetrizing sur tous les indices covariants.

Quelle est la différence entre le delta de Dirac et le delta de Kronecker ?

Kronecker delta δij : Prend en entrée (généralement en MQ) deux entiers i et j, et crache 1 s’ils sont identiques et 0 s’ils sont différents. Notez que i et j sont des entiers comme tels dans un espace discret. Distribution delta de Dirac δ(x) : Prend en entrée un nombre réel x, « crache l’infini » si x=0, sinon sort 0.

Comment fonctionne le delta de Kronecker ?

La fonction delta de Kronecker compare des valeurs (généralement discrètes) et renvoie 1 si elles sont toutes identiques, sinon elle renvoie 0. Dit autrement, si toutes les différences des arguments sont 0, alors la fonction renvoie 1.

Qu’est-ce que la matrice delta ?

linear-algebra. Le delta de Kronecker est défini comme suit : δmn={1if m=n,0if m≠n. Cela est égal à la matrice En qui est une matrice dont la diagonale est remplie de uns.

Qu’est-ce qu’un tenseur en maths ?

En mathématiques, un tenseur est un objet algébrique qui décrit une relation multilinéaire entre des ensembles d’objets algébriques liés à un espace vectoriel. Les tenseurs sont définis indépendamment de toute base, bien qu’ils soient souvent désignés par leurs composantes dans une base liée à un système de coordonnées particulier.

Qu’est-ce que la transformée de Fourier d’une fonction delta ?

La transformée de Fourier d’une fonction (par exemple, une fonction de temps ou d’espace) fournit un moyen d’analyser la fonction en termes de ses composantes sinusoïdales de différentes longueurs d’onde. La fonction elle-même est une somme de ces composantes. La fonction delta de Dirac est une fonction très localisée qui est nulle presque partout.

Le delta de Kronecker est-il invariant ?

Le delta de Kronecker est le seul tenseur de second rang isotrope. Il est assez simple de prouver que le delta de Kronecker est un tenseur isotrope, c’est-à-dire invariant par rotation.

Le delta de Kronecker est-il l’identité ?

Propriétés de la fonction delta

Une autre pratique courante consiste à représenter les séquences discrètes par des crochets ; ainsi : δ[n]. Le delta de Kronecker n’est pas le résultat de l’échantillonnage direct de la fonction delta de Dirac. Le delta de Kronecker forme l’élément d’identité multiplicatif d’une algèbre d’incidence.

Quelle est la différence entre la matrice unitaire et la matrice identité ?

Il y a deux significations populaires pour le mot « identité » dans la langue anglaise. Par conséquent, ce type de matrice est appelé une matrice d’identité, et simplement dénoté par en mathématiques. Elle est également appelée matrice unitaire. Une matrice identité est fondamentalement une matrice carrée.

Le produit de kronecker est-il commutatif ?

Le produit de Kronecker n’est pas commutatif, c’est-à-dire que généralement A ⊗ B ≠ B ⊗ A .

Comment écrit-on un tenseur ?

La curl d’un vecteur s’écrit en notation tensorielle comme ϵijkvk,j ϵ i j k v k , j . Il est essentiel de reconnaître que le vecteur est écrit comme vk,j v k , j ici, et non vj,k v j , k . Cela est dû au fait que la curle est ∇×v ∇ × v , et non v×∇ v × ∇ .

A quoi sert la fonction delta de Dirac ?

Le delta de Dirac est utilisé pour modéliser une fonction de pointe étroite et haute (une impulsion), et d’autres abstractions similaires telles qu’une charge ponctuelle, une masse ponctuelle ou un point électronique. Par exemple, pour calculer la dynamique d’une boule de billard frappée, on peut approximer la force de l’impact par une fonction delta.

Quelle est la signification de la notation indicielle ?

Définition de la notation indicielle. La notation indicielle est une méthode de représentation des chiffres et des lettres qui ont été multipliés par eux-mêmes plusieurs fois. Par exemple, le nombre 360 peut être écrit sous la forme 2×2×2×3×3×5. ou 23×33×5.

Le symbole de Levi Civita est-il un tenseur ?

[edit] Le symbole de Levi-Civita est-il un tenseur ? Dans la conception du physicien, un tenseur est caractérisé par son comportement sous des transformations entre bases d’un certain espace linéaire sous-jacent. Si l’on considère les transformations de base les plus générales, la réponse est non, le symbole de Levi-Civita n’est pas un tenseur.

Pourquoi le delta de Dirac n’est-il pas une fonction ?

Pourquoi la fonction delta de Dirac n’est pas une fonction :

L’aire sous gσ(x) est égale à 1, pour toute valeur de σ. > 0, et gσ(x) s’approche de 0 comme σ → 0 pour tout x autre que x = 0. Puisque ϵ peut être choisi aussi petit que l’on veut, l’aire sous la fonction limite g(x) doit être nulle. l’intégrande d’abord, et intègre ensuite, la réponse est zéro.

Qu’est-ce qu’un tenseur mixte de second rang ?

En analyse tensorielle, un tenseur mixte est un tenseur qui n’est ni strictement covariant ni strictement contravariant ; au moins un des indices d’un tenseur mixte sera un indice (covariant) et au moins un des indices sera un exposant (contravariant).

Qu’entend-on par transformée de Fourier ?

La transformée de Fourier est une méthode mathématique qui exprime une fonction comme la somme de fonctions sinusoïdales (ondes sinusoïdales). Les transformées de Fourier sont largement utilisées dans de nombreux domaines des sciences et de l’ingénierie, notamment le traitement des images, la mécanique quantique, la cristallographie, les géosciences, etc.

Pourquoi la transformée de Fourier de la fonction delta est-elle égale à 1 ?

L’intuition physique est que la « fonction delta » est « infiniment concentrée » dans le domaine temporel, donc sa transformée de Fourier devrait être « complètement étalée » dans le domaine fréquentiel. pour tout f∈S. Par conséquent, ˜δ=1.

Quelle est la transformée de Fourier inverse de la fonction delta ?

Puisque ⟨ δ , f ⟩ = f ( 0 ) langle delta,f rangle = f(0) ⟨δ,f⟩=f(0) (c’est la définition de δ), la transformée de Fourier inverse unitaire du delta de Dirac est une distribution qui, étant donné une fonction f, évalue la transformée de Fourier de f à zéro.