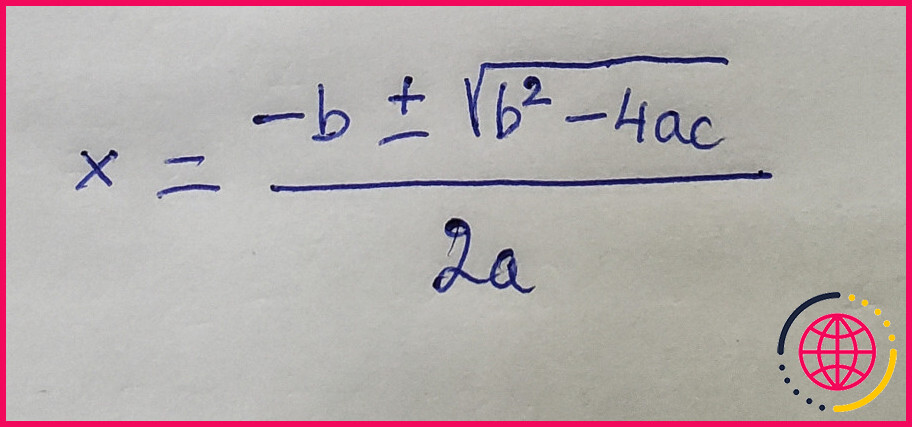Le discriminant inclut-il la racine carrée ?

Le discriminant d’un polynôme est une quantité qui permet de déterminer le nombre et le type de solutions à l’équation $f(x) = 0$. En général, le discriminant est une fonction des coefficients du polynôme et il peut donc être difficile à calculer. Cependant, pour certains cas particuliers, comme lorsque le polynôme ne comporte que deux termes, le discriminant peut être écrit sous une forme simplifiée.

• En particulier, lorsque le polynôme n’a que deux termes, le discriminant est donné par : $$Delta = b^2 4ac$$
• où $a$, $b$ et $c$ sont les coefficients du polynôme. Cette formule est dérivée du fait que les racines d’une équation quadratique sont données par : $$x = frac{b pm sqrt{Delta}}{2a}$$

Ainsi, on peut voir que si $Delta 0$ alors il y a deux racines réelles distinctes. En d’autres termes, le signe de $Delta$ détermine s’il existe ou non des solutions réelles à l’équation.

Fait intéressant, nous pouvons également utiliser cette formule pour déterminer si un polynôme donné a ou non des racines complexes. En particulier, si nous insérons des nombres complexes pour $a$, $b$ et $c$ dans la formule pour $Delta$, nous constatons que : $$Delta = b^2 – 4ac = (b – 2a sqrt{c}) (b + 2asqrt{c})$$.

Ainsi, on voit que si $sqrt{c}$ n’est pas un nombre réel alors $Delta$ sera négatif et donc il n’y aura pas de racines complexes. D’autre part, si $sqrt{c}$ est un nombre réel alors $Delta geq 0$ et donc il peut y avoir des racines complexes. Par conséquent, nous pouvons conclure que le fait qu’un polynôme ait ou non des racines complexes dépend du fait que son discriminant inclut ou non une racine carrée.

Le discriminant est la partie de la formule quadratique située sous le symbole de la racine carrée : b²-4ac. Le discriminant nous indique s’il y a deux solutions, une solution ou aucune solution.

Combien de racines y a-t-il dans le discriminant ?

Pour l’équation quadratique ax2 + bx + c = 0, l’expression b2 – 4ac est appelée le discriminant. La valeur du discriminant indique combien de racines possède f(x) : – Si b2 – 4ac > 0, alors la fonction quadratique a deux racines réelles distinctes. – Si b2 – 4ac = 0 alors la fonction quadratique a une racine réelle répétée.

Quel est le discriminant d’une équation ?

Discriminant, en mathématiques, un paramètre d’un objet ou d’un système calculé comme une aide à sa classification ou à sa solution. Dans le cas d’une équation quadratique ax…² + bx + c = 0, le discriminant est b² – 4ac; pour une équation cubique x³ + ax² + bx + c = 0, le discriminant est a²b² + 18abc – 4b³ – 4a³c – 27c^2.

Pourquoi l’appelle-t-on le discriminant ?

L’argument (c’est-à-dire le contenu) de la racine carrée, étant l’expression b.² – 4ac, est appelé le « discriminant » car, en utilisant sa valeur, on peut « discriminer » entre (c’est-à-dire être capable de faire la différence entre) les différents types de solutions.

Que se passe-t-il si le discriminant est égal à 0 ?

Si le discriminant est égal à zéro, cela signifie que l’équation quadratique a deux racines réelles et identiques. Par conséquent, il y a deux racines réelles et identiques à l’équation quadratique x.² + 2x + 1. D > 0 signifie deux racines réelles et distinctes. D < 0 signifie qu’il n’y a pas de racines réelles.

Quand faut-il utiliser le discriminant ?

Utilisez le discriminant pour déterminer si une équation quadratique a deux solutions réelles, une solution réelle ou deux solutions complexes.

Que sont les racines réelles et distinctes ?

Si une équation a des racines réelles, alors les solutions ou racines de l’équation appartiennent à l’ensemble des nombres réels. Si l’équation a des racines distinctes, alors on dit que toutes les solutions ou racines des équations ne sont pas égales. Lorsqu’une équation quadratique a un discriminant supérieur à 0, alors elle a des racines réelles et distinctes.

Pourquoi est-il important d’obtenir le discriminant ?

Le discriminant de l’équation quadratique est important car il nous indique le nombre et le type de solutions. Cette information est utile car elle sert de double vérification lors de la résolution d’équations quadratiques par l’une des quatre méthodes (factorisation, complétion du carré, utilisation des racines carrées et utilisation de la formule quadratique).

Que faire si le discriminant est négatif ?

Le discriminant est le terme sous la racine carrée dans la formule quadratique et nous indique le nombre de solutions à une équation quadratique. Si le discriminant est positif, nous savons que nous avons 2 solutions. S’il est négatif, il n’y a pas de solutions et si le discriminant est égal à zéro, nous avons une solution.

Est-ce que 1 est un carré parfait ?

De manière informelle : Lorsque l’on multiplie un nombre entier (un nombre « entier », positif, négatif ou nul) par lui-même, le produit obtenu est appelé un nombre carré, ou un carré parfait ou simplement « un carré ». Ainsi, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, et ainsi de suite, sont tous des nombres carrés.

Qu’est-ce que la valeur discriminante ?

Définition de la valeur discriminante

Un discriminant est une fonction des coefficients d’une équation polynomiale qui exprime la nature des racines de l’équation quadratique donnée. Lorsque la valeur du discriminant est positive, on obtient deux solutions réelles. Lorsque la valeur du discriminant est nulle, on obtient une solution réelle.

Que se passe-t-il lorsque B 2 4ac 0 ?

Polynômes quadratiques

La quantité b²-4ac est appelée le discriminant du polynôme. Si b²-4ac < 0 l’équation n’a pas de solutions en nombres réels, mais elle a des solutions complexes. Si b²-4ac = 0, l’équation a une racine réelle répétée. Si b²-4ac > 0 l’équation a deux racines réelles distinctes.

Que signifie 2 racines égales ?

Si la fonction f(x) est une quadratique ou a une puissance supérieure à 1, il y a deux racines. Ces deux racines sont donc égales. par exemple, les racines de. x^2 + 6x +9.

Comment savoir si les racines sont imaginaires ?

Les racines imaginaires apparaissent dans une équation quadratique lorsque le discriminant de l’équation quadratique – la partie située sous le signe de la racine carrée (b² – 4ac) – est négative. Si cette valeur est négative, vous ne pouvez pas réellement prendre la racine carrée, et les réponses ne sont pas réelles.

Lorsque le discriminant 0 alors les racines sont ?

De toute évidence, le discriminant de l’équation quadratique donnée est nul. Par conséquent, les racines sont réelles et égales.

Quel est le discriminant de 3x 2 10x =- 2 ?

Trouver le discriminant de 3×2-10x=-2.

Trouver : Le discriminant ? Ici, a=3, b=-10 et c=2. Substituez les valeurs, Par conséquent, le discriminant de est 76.

Combien de solutions réelles y a-t-il si la valeur de k 0 ?

(Si k =0, il n’y a qu’une seule solution distincte, parfois appelée solution double).

Que signifie un discriminant de 1 ?

Si le discriminant est égal à 0, l’équation quadratique a 1 solution réelle. Si le discriminant est inférieur à 0, l’équation quadratique a 0 solutions réelles. (Au lieu de solutions réelles, l’équation quadratique a 2 solutions imaginaires). Source de l’image : Par Expii. 1.

Quel est un autre mot pour discriminant ?

Dans cette page, vous pouvez découvrir 12 synonymes, antonymes, expressions idiomatiques et mots connexes pour discriminant, comme : univarié, pgcd, , chi-carré, valeur réelle, bivarié, glm, variate, PARAFAC, paramétrique et validation croisée.

Combien de racines si le discriminant est négatif ?

Si le discriminant est positif, alors vous avez , ce qui conduit à deux réponses en nombres réels. S’il est négatif, on a , ce qui donne deux résultats complexes. Et si b² – 4ac est 0, alors vous avez , donc vous n’avez qu’une seule solution.