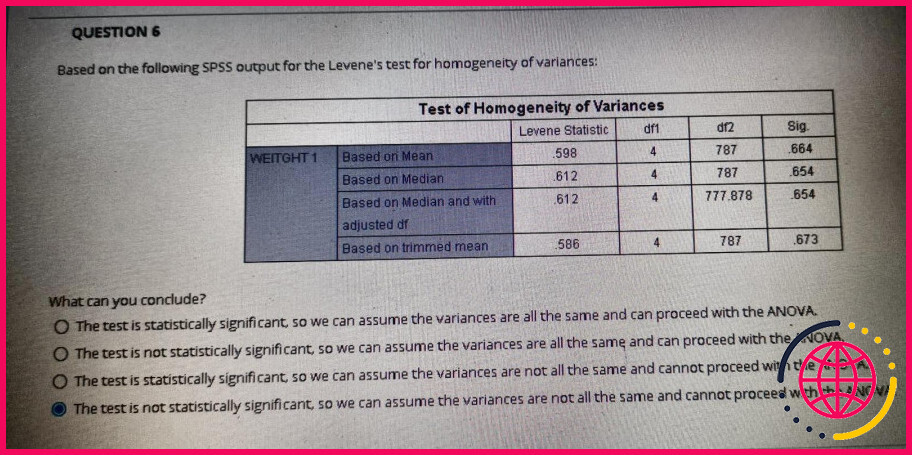
Le test de Levene doit-il être significatif ?

Il y a un certain nombre de choses à considérer pour déterminer si le test de Levene doit être significatif ou non. Le premier est la nature des données analysées. Si les données sont vraiment homogènes, le test de Levene ne devrait pas être nécessaire. Cependant, si les données sont hétérogènes, le test de Levene peut être utilisé pour déterminer si les variances sont égales.

Une autre considération est la taille de l’échantillon. Si la taille de l’échantillon est suffisamment grande, le test de Levene peut ne pas être nécessaire. Cependant, si la taille de l’échantillon est petite, le test de Levene peut aider à garantir que les résultats ne sont pas biaisés par des valeurs aberrantes.

Enfin, il est également important de considérer la puissance du test. Si la puissance du test est trop faible, il se peut qu’il ne soit pas en mesure de détecter des différences significatives de variance. D’autre part, si la puissance du test est trop élevée, il peut produire des faux positifs.

En général, le test de Levene doit être utilisé lorsqu’il y a des raisons de croire que les variances ne sont pas égales. Au moment de décider d’utiliser ou non le test de Levene, tous ces facteurs doivent être pris en compte afin de prendre une décision éclairée.

Le test de levene permet de vérifier l’égalité des variances. Une valeur p non significative du test de levene montre que les variances sont bien égales et qu’il n’y a pas de différence entre les variances des deux groupes. Donc, vous devriez vous fier et rapporter seulement la valeur p obtenue du test t des échantillons indépendants et non du test de levene.

Que faire si le test de Levene est significatif dans l’Anova ?

Dans ce cas, le test de Levene teste si les variances des quatre groupes sont significativement différentes. ® Si le test de Levene est significatif (c’est-à-dire que la valeur de sig. est inférieure à . 05) alors nous pouvons conclure que les variances sont significativement différentes. On peut aussi regarder le rapport des variances.

Comment savoir si le test de Levene est significatif ?

Ensuite, la taille de nos échantillons est fortement inégale donc nous devons vraiment répondre à l’hypothèse d’homogénéité des variances. Cependant, le test de Levene est statistiquement significatif car son p < 0,05 : nous rejetons son hypothèse nulle d’égalité des variances de la population.

Que montre le test de Levene ?

En statistique, le test de Levene est une statistique inférentielle utilisée pour évaluer l’égalité des variances d’une variable calculée pour deux ou plusieurs groupes. Il teste l’hypothèse nulle selon laquelle les variances de la population sont égales (appelée homogénéité de la variance ou homoscédasticité).

Que se passe-t-il si le test de Levene n’est pas significatif ?

Le test de levene permet de vérifier l’égalité des variances. Une valeur p non significative du test de Levene montre que les variances sont bien égales et qu’il n’y a pas de différence entre les variances des deux groupes.

Que représente la valeur P du test de Levene ?

Pour ce test, une valeur p inférieure à 0,05 indique qu’il y a, en fait, suffisamment de variance dans l’échantillon pour tenir compte des éventuelles différences de moyenne. La valeur p indiquée pour le test de Levene pour l’égalité de la variance dans le tableau ci-dessus est p = 0,000, ce qui est bien inférieur au seuil de 0,05.

Quand faut-il utiliser le test de Levene ?

Le test de Levene ( Levene 1960) est utilisé pour tester si k échantillons ont des variances égales. L’égalité des variances entre les échantillons est appelée homogénéité de la variance. Certains tests statistiques, par exemple l’analyse de la variance, supposent que les variances sont égales entre les groupes ou les échantillons. Le test de Levene peut être utilisé pour vérifier cette hypothèse.

Comment savoir si vous avez une homogénéité de la variance ?

Parmi ces tests, l’évaluation la plus courante de l’homogénéité de la variance est le test de Levene. Le test de Levene utilise un test F pour tester l’hypothèse nulle selon laquelle la variance est égale entre les groupes. Une valeur p inférieure à . 05 indique une violation de l’hypothèse.

Quand dois-je ignorer le test de Levene ?

Vous pouvez ignorer cette hypothèse si vous avez des tailles d’échantillon à peu près égales pour chaque groupe. Cependant, si vous avez des tailles d’échantillons nettement différentes, alors vous devez effectivement vous assurer que l’homogénéité des variances est respectée par vos données.

Quelle est la différence entre le test F de l’Anova à sens unique et le test de Levene ?

Une méthode est le test de Bartlett pour l’homogénéité de la variance (ce test est très sensible à la non-normalité). Le test F de Levene pour l’égalité des variances, qui est la statistique la plus utilisée (et qui est fournie dans SPSS), est utilisé pour tester l’hypothèse d’homogénéité de la variance.

Comment signaler un test de Levene significatif ?

Si le test de Levene pour l’égalité des variances est significatif, rapportez les statistiques pour la ligne variances égales non supposées avec les degrés de liberté modifiés arrondis au nombre entier le plus proche.

Comment savoir si la variance est significative ?

Si la valeur p est inférieure à votre niveau de signification (par exemple, 0,05), vous pouvez rejeter l’hypothèse nulle. La différence entre les deux variances est statistiquement significative. Cette condition indique que votre échantillon fournit des preuves suffisamment fortes pour conclure que la variabilité des deux populations est différente.

Pourquoi est-il important de tester l’homogénéité de la variance ?

L’hypothèse d’homogénéité de la variance est importante pour que l’estimation groupée puisse être utilisée. Cependant, lorsque la taille des échantillons est inégale, la mise en commun des variances peut donner des résultats très différents. Test de l’homogénéité de la variance. Lors du test de l’homogénéité de la variance, l’hypothèse nulle est .

Comment tester l’homogénéité ?

Dans le test d’homogénéité, nous sélectionnons des échantillons aléatoires de chaque sous-groupe ou population séparément et recueillons des données sur une seule variable catégorielle. L’hypothèse nulle dit que la distribution de la variable catégorielle est la même pour chaque sous-groupe ou population. Les deux tests utilisent la même statistique de test du chi-deux.

Que faire si le Levene est significatif ?

Si ce dernier test est significatif, utilisez le test ANOVA de Welch à la place du test F de l’ANOVA. Si vous avez des données non normales mais des variances de population égales, utilisez le test de Kruskal-Wallis sur les rangs.

Quels sont les deux types de variance qui peuvent apparaître dans vos données ?

Quels sont les deux types de variances qui peuvent apparaître dans vos données ? ANOVA et ANCOVA/expérimentateur et participant/entre et au sein du groupe/indépendant et confusionnel.

Que se passe-t-il si l’homogénéité de la variance n’est pas respectée ?

Ainsi, si vos groupes ont des écarts types très différents et ne conviennent donc pas à l’ANOVA à sens unique, ils ne doivent pas non plus être analysés par le test de Kruskal-Wallis ou de Mann-Whitney. La meilleure approche consiste souvent à transformer les données. Souvent, la transformation en logarithmes ou en réciprocité fait l’affaire, en rétablissant l’égalité de la variance.

La valeur P est-elle statistiquement significative ?

Une valeur p inférieure à 0,05 (généralement ≤ 0,05) est statistiquement significative. Une valeur p supérieure à 0,05 (> 0,05) n’est pas statistiquement significative et indique une forte évidence pour l’hypothèse nulle. Cela signifie que nous retenons l’hypothèse nulle et rejetons l’hypothèse alternative.

Que signifie une valeur P supérieure à 0,05 ?

P > 0,05 est la probabilité que l’hypothèse nulle soit vraie. Un résultat de test statistiquement significatif (P ≤ 0,05) signifie que l’hypothèse de test est fausse ou doit être rejetée. Une valeur P supérieure à 0,05 signifie qu’aucun effet n’a été observé.

Qu’est-ce que l’exemple de la valeur p ?

Définition de la valeur P

Une valeur p est utilisée dans les tests d’hypothèse pour vous aider à soutenir ou à rejeter l’hypothèse nulle. La valeur p est la preuve contre une hypothèse nulle. Par exemple, une valeur p de 0,0254 correspond à 2,54 %. Cela signifie qu’il y a 2,54 % de chances que vos résultats soient aléatoires (c’est-à-dire qu’ils soient arrivés par hasard).

Que signifie un test de Welch significatif ?

Le test de Welch pour les variances inégales (également appelé test t de Welch, T ajusté de Welch ou test t pour variances inégales) est une modification du test t de Student pour voir si les moyennes de deux échantillons sont significativement différentes. L’hypothèse nulle du test est que les moyennes sont égales.

Quelle est la signification d’une variance de coût significative ?

Définition : Un écart de coût est la différence entre les dépenses réelles engagées et les dépenses standard estimées au début d’une période. La direction utilise ces écarts pour analyser et suivre l’évolution des processus de production, des budgets et d’autres opérations.

Qu’est-ce qu’un écart de coût significatif ?

En général, un écart de coût est la différence entre le montant réel d’un coût et son montant budgété ou planifié. Lorsque le coût réel est supérieur au montant budgété, l’écart de coût est dit défavorable. Lorsqu’un coût réel est inférieur au montant budgété, l’écart de coût est dit favorable.

Comment savoir si la valeur F est significative ?

Si vous obtenez une grande valeur f (une qui est plus grande que la valeur critique F trouvée dans un tableau), cela signifie que quelque chose est significatif, tandis qu’une petite valeur p signifie que tous vos résultats sont significatifs. La statistique F ne fait que comparer l’effet conjoint de toutes les variables ensemble.