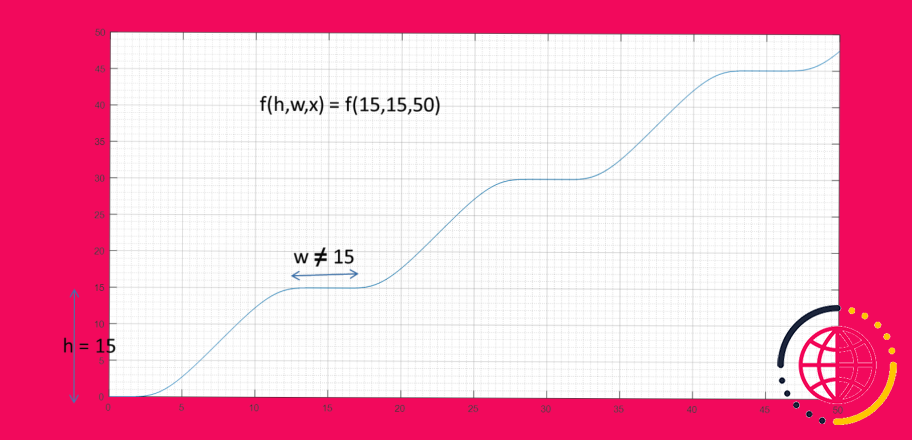
Quand une fonction est-elle lisse ?

Une fonction est lisse si elle est continue et différentiable. L’exigence de dérivabilité signifie que la fonction doit se comporter correctement dans le sens où sa dérivée existe et est elle-même une fonction continue.

Pour qu’une fonction soit lisse, elle doit avoir des dérivées continues jusqu’à un certain ordre, dit k. On dit que cette fonction est Ck lisse. Un exemple de fonction continue mais non lisse est la valeur absolue, qui est continue partout mais non différentiable partout. Une fonction lisse est différentiable
Une fonction est différentiable
En calcul (une branche des mathématiques), une fonction différentiable d’une variable réelle est une fonction dont la dérivée existe en chaque point de son domaine. Plus généralement, pour x est un point intérieur du domaine d’une fonction f, alors on dit que f est différentiable en x si et seulement si la dérivée f ′(x) existe.
https://en.wikipedia.org ‘ wiki ‘ Fonction_différentiable

Fonction différentiable – Wikipédia.

Comment savoir si une fonction est lisse ?

Prouvez que f(x)=1x est lisse (infiniment différentiable).

La seule fonction qui me vient à l’esprit qui soit lisse est g(x)=ex, car elle est définie sur tout R, continue partout, et une fois que vous avez prouvé que g′(x)=ex, vous avez fini de montrer qu’elle est infiniment différentiable, c’est-à-dire lisse.

Quelles fonctions sont lisses ?

Les fonctions lisses ont une dérivée première définie unique (pente ou gradient) en chaque point. Graphiquement, une fonction lisse d’une seule variable peut être tracée comme une seule ligne continue sans courbes ou ruptures abruptes.

Comment savoir si une courbe est lisse ?

Une courbe définie par x=f(t),y=g(t) est lisse si f′(x) et g′(x) sont continues et non simultanément nulles.

Que signifie le fait qu’un graphique soit lisse ?

On dit qu’une courbe est lisse si chaque point a un voisinage sur lequel la courbe est le graphe d’une fonction différentiable. Il y a deux façons évidentes pour une courbe de ne pas être lisse : (1) elle peut se couper elle-même, ou (2) elle peut avoir une cuspide. Exemple d’une courbe lisse : Soit S = F(x, y) = y – x2 = 0.

Qu’est-ce qu’un exemple lisse ?

La définition de lisse est égale, plate et non rugueuse. Un exemple de lisse est la peau d’un bébé. Un exemple de lisse est une sauce sans grumeaux.

Qu’est-ce que cela signifie de dire qu’une fonction est lisse ?

En analyse mathématique, le caractère lisse d’une fonction est une propriété mesurée par le nombre de dérivées continues qu’elle possède sur un certain domaine. Au minimum, une fonction pourrait être considérée comme lisse si elle est différentiable partout (donc continue).

Comment savoir si un vecteur est lisse ?

Une fonction à valeur vectorielle r(t) définie sur un intervalle I est lisse si r a une dérivée continue sur I et r (t) = 0 pour chaque point intérieur t. Une courbe C est lisse si elle a une paramétrisation lisse. Exemple Considérons la courbe paramétrée par r(t) = t3i + t2j.

Comment fait-on pour lisser une courbe ?

Lisser une courbe

1. Sélectionnez la courbe, ou sélectionnez uniquement les CV que vous souhaitez lisser.
2. Sélectionner les courbes > Lisser . Pour contrôler la quantité de lissage, choisissez Courbes. > Lisser > et définissez l’option Lissage. Les valeurs plus faibles font moins de lissage. La valeur par défaut est de 10.

Quelle est la fonction principale du muscle lisse ?

La fonction principale du muscle lisse est la contraction. Les muscles lisses sont de deux types : à unité unique et à unités multiples. Le muscle lisse à unité unique est constitué de plusieurs cellules connectées par des connexines qui peuvent être stimulées de manière synchrone à partir d’une seule entrée synaptique.

Les polynômes sont-ils lisses ?

Solution. Les graphes de f et h sont des graphes de fonctions polynomiales. Ils sont lisses et continus.

Qu’est-ce qu’une frontière lisse ?

Géométrie différentielle. Soit M⊂Rn un collecteur de dimension k et X⊂M un sous-ensemble. La frontière de X dans M, notée ∂MX, est l’ensemble de tous les x∈X tels que chaque nuage voisin de x contient des points dans X et M∖X.

Qu’est-ce que la règle de lissage ?

– Règle de lissage : Si t(n) ∈ Θ(f(n)|n = b. k. ) et f est lisse. et t est éventuellement non décroissante, alors t(n) ∈ Θ(f(n)) sans condition.

Qu’est-ce qu’une courbe lisse ?

Une courbe lisse est une courbe qui est une fonction lisse, où le mot « courbe » est interprété dans le contexte de la géométrie analytique. En particulier, une courbe lisse est une carte continue d’un espace unidimensionnel à un espace . -dimensionnel qui sur son domaine a des dérivées continues jusqu’à un ordre désiré.

Qu’est-ce qu’une courbe C1 ?

C1 signifie dérivée 1ère continue. Donc si vous calculez la dérivée numériquement et que vous voyez ensuite de grands sauts dans la dérivée alors vous pouvez suspecter que la courbe sous-jacente n’est pas C1.

Comment lisser une fonction ?

Dans le lissage, les points de données d’un signal sont modifiés de sorte que les points individuels plus élevés que les points adjacents (vraisemblablement à cause du bruit) sont réduits, et les points qui sont plus bas que les points adjacents sont augmentés conduisant à un signal plus lisse.

Comment lisser un ensemble de données ?

Le lissage des données peut être défini comme une approche statistique consistant à éliminer les valeurs aberrantes des ensembles de données pour rendre les modèles plus perceptibles. La méthode aléatoire, la moyenne mobile simple, la marche aléatoire, l’exponentielle simple et la moyenne mobile exponentielle sont quelques-unes des méthodes utilisées pour le lissage des données.

Qu’est-ce que la demande lissée ?

Utilisé en marketing lorsque la demande dépasse la production les annonces et le matériel promotionnel sont retirés du marché jusqu’à ce que la production ait rattrapé son retard.

Qu’est-ce qu’une courbe simple ?

: un arc de cercle (comme celui d’une voie ferrée) joignant deux tangentes – comparer avec la courbe composée.

Qu’est-ce qu’un domaine lisse ?

Définition 6.43. Un sous-ensemble fermé D ⊆ X est un domaine lisse si pour tout point. p ∈ Bd (D), il existe une paramétrisation φ : U → V de X en p telle que φ(U ∩

Qu’est-ce qu’une courbe régulière ?

Une courbe différentiable est dite régulière si sa dérivée ne disparaît jamais. ( En d’autres termes, une courbe régulière ne ralentit jamais jusqu’à un arrêt ou ne revient pas sur elle-même.) Deux courbes différentiables et. sont dites équivalentes s’il existe une carte bijective. telle que la carte inverse.

Qu’est-ce qu’une solution lisse ?

Une solution lisse est une solution dont les dérivées sont infiniment nombreuses. Une solution lisse est classique, mais une solution classique peut ne pas être lisse.

Un graphe est-il lisse ?

Graphiquement, une fonction lisse d’une seule variable peut être tracée comme une seule ligne continue sans courbes ou ruptures abruptes. Peut-être encore plus déroutantes que les fonctions avec des courbes abruptes sont les fonctions discontinues qui ont des ruptures réelles dans leurs graphiques. Les fonctions discontinues dans LINGO incluent @SIGN et @FLOOR.