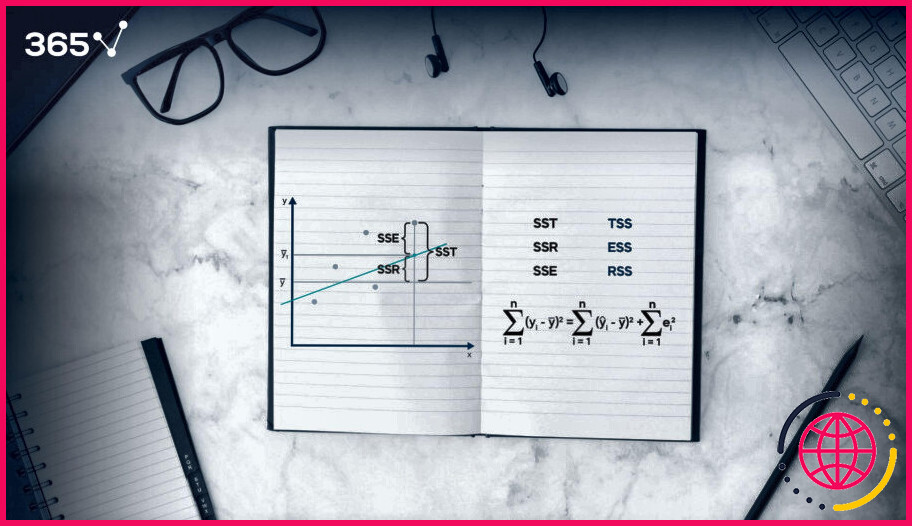
Que signifie la somme des carrés ?

La somme des carrés est une technique statistique utilisée dans l’analyse de régression pour déterminer la dispersion des points de données. La somme des carrés est utilisée comme moyen mathématique pour trouver la fonction qui s’ajuste le mieux (varie le moins) à partir des données.

À ce propos, que représente la somme des carrés ?

La somme des carrés représente une mesure de la variation ou de l’écart par rapport à la moyenne . Elle est calculée comme une sommation des carrés des différences par rapport à la moyenne .

De même, comment calcule-t-on la somme des carrés ? Pour calculer celle-ci, il faut soustraire le nombre de groupes du nombre global d’individus. La SS _in est la somme des carrés à l’intérieur des groupes. La formule est : degrés de liberté pour chaque groupe individuel (n-1) * somme des carrés écart type pour chaque groupe.

De même, on peut se demander ce que signifie la somme des carrés dans l’Anova.

Dans le contexte de l’ ANOVA , cette quantité est appelée la somme des carrés totale (abrégée SS_T) car elle se rapporte à la variance totale des observations. Ainsi : Le dénominateur dans la relation de la variance de l’échantillon est le nombre de degrés de liberté associé à la variance de l’échantillon.

Que signifie l’erreur de la somme des carrés ?

Erreur somme des carrés . Somme des carrés des erreurs (SSE) La SSE est la somme des différences carrées entre chaque observation et la moyenne de son groupe. Elle peut être utilisée comme une mesure de la variation au sein d’une grappe. Si tous les cas au sein d’une grappe sont identiques, la SSE serait alors égale à 0,

.

Qu’est-ce que l’ESS dans l’analyse de régression ?

La somme des carrés ( SS ) est un outil statistique qui est utilisé pour identifier la dispersion des données ainsi que la façon dont les données peuvent s’adapter au modèle dans l’analyse de régression . Elle peut être utilisée pour évaluer la force de la relation entre les variables et pour modéliser la relation future entre elles..

.

Qu’est-ce que le SSM en statistique ?

n est le nombre d’observations, p est le nombre de paramètres de régression. Somme corrigée des carrés du modèle : SSM = Σ _i=1 ⁿ (y _i^ – y) ², aussi appelée somme des carrés pour la régression. Pour les modèles de régression multiple, nous avons cette propriété remarquable : SSM + SSE = SST.

Pourquoi la somme des carrés est-elle importante ?

En plus de vous dire simplement combien de variation il y a dans un ensemble de données, la somme des carrés est utilisée pour calculer d’autres mesures statistiques, telles que la variance, l’erreur standard et l’écart type. Celles-ci fournissent des informations importantes sur la façon dont les données sont distribuées et sont utilisées dans de nombreux tests statistiques.

La somme des carrés est-elle la variance ?

A mesure que l’on ajoute des points de données à l’ensemble, la somme des carrés devient plus grande car les valeurs seront plus étalées. La variance est la moyenne de la somme des carrés (c’est-à-dire la somme des carrés divisée par le nombre d’observations). L’écart-type est la somme des carrés racine de la variance .

La somme des carrés peut-elle être négative ?

SS = Σ(X – )2. Quand on élève au carré un nombre réel, le résultat est toujours non négatif . La somme de nombres non négatifs doit être non négative . La seule façon dont chaque score d’écart carré peut être égal à 0 est si tous les scores sont égaux à la moyenne.

Qu’est-ce que la formule Anova ?

Formule Anova . L’analyse de la variance, ou ANOVA , est une technique statistique forte qui est utilisée pour montrer la différence entre deux ou plusieurs moyennes ou composantes par des tests de signification. Elle nous montre également un moyen de faire des comparaisons multiples de plusieurs moyennes de population.

Qu’est-ce que le F dans le tableau Anova ?

Le rapport F est le rapport de deux valeurs quadratiques moyennes. Si l’hypothèse nulle est vraie, vous vous attendez à ce que le F ait une valeur proche de 1,0 la plupart du temps. Un grand rapport F signifie que la variation entre les moyennes des groupes est plus importante que ce que vous vous attendez à voir par hasard.

Comment trouver la somme des carrés des erreurs ?

Pour calculer la somme des carrés pour l’erreur , commencez par trouver la moyenne de l’ensemble des données en additionnant toutes les valeurs et en divisant par le nombre total de valeurs. Ensuite, soustrayez la moyenne de chaque valeur pour trouver l’écart de chaque valeur. Ensuite, mettez au carré l’écart de chaque valeur.

Comment interpréter le carré moyen d’Anova ?

ANOVA

1. Le carré moyen du traitement est obtenu en divisant la somme des carrés du traitement par les degrés de liberté. Le carré moyen du traitement représente la variation entre les moyennes de l’échantillon.
2. Le carré moyen de l’erreur (MSE) est obtenu en divisant la somme des carrés de l’erreur résiduelle par les degrés de liberté.

Que signifient SS et MS dans le tableau d’Anova ?

Moyens carrés Chaque valeur de moyens carrés est calculée en divisant une valeur de somme des carrés par les degrés de liberté correspondants. En d’autres termes, pour chaque ligne du tableau ANOVA , divisez la valeur SS par la valeur du df pour calculer la valeur MS .

Comment trouver la somme des carrés dans un tableau d’Anova ?

(1) La moyenne Somme des carrés entre les groupes, notée MSB, est calculée en divisant la Somme des carrés entre les groupes par les degrés de liberté entre les groupes. C’est-à-dire, MSB = SS(Between)/(m-1).

Comment interpréter les résultats de l’Anova ?

Interprétez les principaux résultats de l’ANOVA à une voie

1. .

   Étape 1 : Déterminer si les différences entre les moyennes des groupes sont statistiquement significatives.

2. Étape 2 : Examinez les moyennes des groupes.
3. Étape 3 : Comparez les moyennes des groupes.
4. Étape 4 : Déterminez si le modèle s’adapte bien à vos données.
5. Étape 5 : Déterminez si votre modèle répond aux hypothèses de l’analyse.

Quelle est la somme des n premiers carrés ?

Somme des Carrés des Premiers n entiers positifs (k-1)3=k3-3k2+3k-1.

Quelle est la formule de la somme des carrés en statistique ?

Somme des carrés Calculatrice. La moyenne de la somme des carrés (SS) est la variance d’un ensemble de scores, et la racine carrée de la variance est son écart-type. Cette calculatrice simple utilise la formule de calcul SS = ΣX² – ((ΣX)² / N) – pour calculer la somme des carrés pour un seul ensemble de scores.

Comment calcule-t-on le SSW ?

Utilisez la formule SST – SSB pour trouver la SSW , ou la somme des carrés au sein des groupes. Figurez les degrés de liberté pour entre les groupes, « dfb », et au sein des groupes, « dfw ». La formule pour entre les groupes est dfb = 1 et pour les groupes internes c’est dfw = 2n-2. Calculez le carré moyen pour les groupes internes, MSW = SSW / dfw.

Quelle est la formule de la somme d’une suite arithmétique ?

La formule de la somme La formule dit que la somme des n premiers termes de notre séquence arithmétique est égale à n divisé par 2 fois la somme de deux fois le terme de début, a, et le produit de d, la différence commune, et de n moins 1. Le n représente le nombre de termes que l’on additionne.

Que dit le carré moyen ?

Les carrés moyens sont des estimations de la variance entre les groupes. Les carrés moyens sont utilisés dans l’analyse de la variance et sont calculés comme une somme de carrés divisée par ses degrés de liberté appropriés. Carré moyen Entre les groupes, comparez les moyennes des groupes à la grande moyenne : ,.

Qu'est-ce que l'ESS dans l'analyse de régression ?","acceptedAnswer": {"@type": "Answer","text": "La somme des carrés (SS) est un outil statistique qui est utilisé pour identifier la dispersion des données ainsi que la façon dont les données peuvent s'adapter au modèle dans l'analyse de régression. Elle peut être utilisée pour évaluer la force de la relation entre les variables et pour modéliser la relation future entre elles.." } }, {"@type": "Question","name": ".

Qu'est-ce que le SSM en statistique ?","acceptedAnswer": {"@type": "Answer","text": "n est le nombre d'observations, p est le nombre de paramètres de régression. Somme corrigée des carrés du modèle : SSM = Σ i=1 n (y i^ - y) 2, aussi appelée somme des carrés pour la régression. Pour les modèles de régression multiple, nous avons cette propriété remarquable : SSM + SSE = SST." } }, {"@type": "Question","name": "Pourquoi la somme des carrés est-elle importante ?","acceptedAnswer": {"@type": "Answer","text": "En plus de vous dire simplement combien de variation il y a dans un ensemble de données, la somme des carrés est utilisée pour calculer d'autres mesures statistiques, telles que la variance, l'erreur standard et l'écart type. Celles-ci fournissent des informations importantes sur la façon dont les données sont distribuées et sont utilisées dans de nombreux tests statistiques." } }, {"@type": "Question","name": "La somme des carrés est-elle la variance ?","acceptedAnswer": {"@type": "Answer","text": "A mesure que l'on ajoute des points de données à l'ensemble, la somme des carrés devient plus grande car les valeurs seront plus étalées. La variance est la moyenne de la somme des carrés (c'est-à-dire la somme des carrés divisée par le nombre d'observations). L'écart-type est la somme des carrés racine de la variance." } }, {"@type": "Question","name": "La somme des carrés peut-elle être négative ?","acceptedAnswer": {"@type": "Answer","text": "SS = Σ(X - )2. Quand on élève au carré un nombre réel, le résultat est toujours nonnégatif. La somme de nombres nonnégatifs doit être nonnégative. La seule façon dont chaque score d'écart carré peut être égal à 0 est si tous les scores sont égaux à la moyenne." } }, {"@type": "Question","name": "Qu'est-ce que la formule Anova ?","acceptedAnswer": {"@type": "Answer","text": "Formule Anova. L'analyse de la variance, ou ANOVA, est une technique statistique forte qui est utilisée pour montrer la différence entre deux ou plusieurs moyennes ou composantes par des tests de signification. Elle nous montre également un moyen de faire des comparaisons multiples de plusieurs moyennes de population." } }, {"@type": "Question","name": "Qu'est-ce que le F dans le tableau Anova ?","acceptedAnswer": {"@type": "Answer","text": "Le rapport F est le rapport de deux valeurs quadratiques moyennes. Si l'hypothèse nulle est vraie, vous vous attendez à ce que le F ait une valeur proche de 1,0 la plupart du temps. Un grand rapport F signifie que la variation entre les moyennes des groupes est plus importante que ce que vous vous attendez à voir par hasard." } }, {"@type": "Question","name": "Comment trouver la somme des carrés des erreurs ?","acceptedAnswer": {"@type": "Answer","text": "Pour calculer la somme des carrés pour l'erreur, commencez par trouver la moyenne de l'ensemble des données en additionnant toutes les valeurs et en divisant par le nombre total de valeurs. Ensuite, soustrayez la moyenne de chaque valeur pour trouver l'écart de chaque valeur. Ensuite, mettez au carré l'écart de chaque valeur. " } }, {"@type": "Question","name": "Que signifient SS et MS dans le tableau d'Anova ?","acceptedAnswer": {"@type": "Answer","text": "Moyens carrés Chaque valeur de moyens carrés est calculée en divisant une valeur de somme des carrés par les degrés de liberté correspondants. En d'autres termes, pour chaque ligne du tableau ANOVA, divisez la valeur SS par la valeur du df pour calculer la valeur MS." } }, {"@type": "Question","name": "Comment trouver la somme des carrés dans un tableau d'Anova ?","acceptedAnswer": {"@type": "Answer","text": "(1) La moyenne Somme des carrés entre les groupes, notée MSB, est calculée en divisant la Somme des carrés entre les groupes par les degrés de liberté entre les groupes. C'est-à-dire, MSB = SS(Between)/(m-1)." } }, {"@type": "Question","name": "Comment interpréter les résultats de l'Anova ?","acceptedAnswer": {"@type": "Answer","text": "Interprétez les principaux résultats de l'ANOVA à une voie" } }, {"@type": "Question","name": "Quelle est la somme des n premiers carrés ?","acceptedAnswer": {"@type": "Answer","text": "Somme des Carrés des Premiers n entiers positifs (k-1)3=k3-3k2+3k-1." } }, {"@type": "Question","name": "Quelle est la formule de la somme des carrés en statistique ?","acceptedAnswer": {"@type": "Answer","text": "Somme des carrés Calculatrice. La moyenne de la somme des carrés (SS) est la variance d'un ensemble de scores, et la racine carrée de la variance est son écart-type. Cette calculatrice simple utilise la formule de calcul SS = ΣX2 - ((ΣX)2 / N) - pour calculer la somme des carrés pour un seul ensemble de scores." } }, {"@type": "Question","name": "Comment calcule-t-on le SSW ?","acceptedAnswer": {"@type": "Answer","text": "Utilisez la formule SST - SSB pour trouver la SSW, ou la somme des carrés au sein des groupes. Figurez les degrés de liberté pour entre les groupes, "dfb", et au sein des groupes, "dfw". La formule pour entre les groupes est dfb = 1 et pour les groupes internes c'est dfw = 2n-2. Calculez le carré moyen pour les groupes internes, MSW = SSW / dfw." } }, {"@type": "Question","name": "Quelle est la formule de la somme d'une suite arithmétique ?","acceptedAnswer": {"@type": "Answer","text": "La formule de la somme La formule dit que la somme des n premiers termes de notre séquence arithmétique est égale à n divisé par 2 fois la somme de deux fois le terme de début, a, et le produit de d, la différence commune, et de n moins 1. Le n représente le nombre de termes que l'on additionne." } }] }