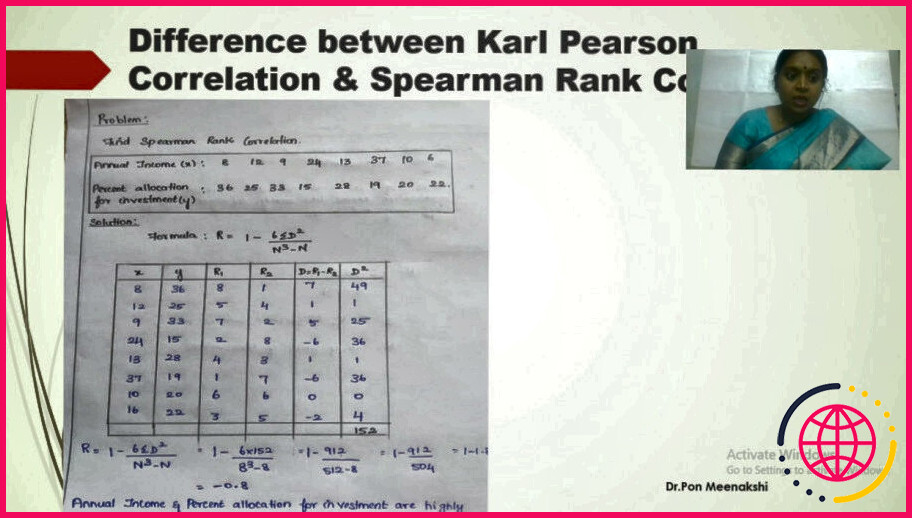
Quelle est la différence entre la corrélation de spearman et de pearson ?

La différence entre la corrélation de Pearson et la corrélation de Spearman est que la Pearson est plus appropriée pour les mesures prises à partir d’une échelle d’intervalle, tandis que la Spearman est plus appropriée pour les mesures prises à partir d’échelles ordinales.

Dans ce contexte, quelle est la différence entre la corrélation de Pearson-Spearman et la corrélation de Kendall ?

Cela signifie que la corrélation de Kendall est préférable lorsqu’il y a de petits échantillons ou quelques valeurs aberrantes. La corrélation de Kendall a une complexité de calcul O(n^2) en comparaison avec O(n logn) de la corrélation de Spearman , où n est la taille de l’échantillon. Le Rho de Spearman est généralement plus grand que le Tau de Kendall .

On peut également se demander quelle est la différence entre la corrélation de Pearson et la corrélation de Spearman quizlet ? Un chercheur évaluant la signification de une corrélation de Pearson obtient r = 0,78 et peut conclure que t = 1,34. quelle est la différence entre la corrélation de Pearson et la corrélation de Spearman ? La corrélation de Spearman est la même que la corrélation de Pearson , mais elle est utilisée sur des données issues d’une échelle ordinale.

De même, pourquoi utiliser le rang de Spearman ?

Le coefficient de corrélation du rang de Spearman est une technique qui peut être utilisée pour résumer la force et la direction (négative ou positive) d’une relation entre deux variables. Le résultat sera toujours compris entre 1 et moins 1. Créez un tableau à partir de vos données. Rank les deux ensembles de données.

Comment interpréter la corrélation de Spearman ?

Le coefficient de corrélation Spearman , r_s, peut prendre des valeurs de +1 à -1. Un r_s de +1 indique une association parfaite des rangs, un r_s de zéro n’indique aucune association entre les rangs et un r_s de -1 indique une association négative parfaite des rangs. Plus r_s est proche de zéro, plus l’association entre les rangs est faible.

Quand dois-je utiliser la corrélation de Spearman ?

La corrélation de Spearman est souvent utilisée pour évaluer les relations impliquant des variables ordinales. Par exemple, vous pourriez utiliser une corrélation de Spearman pour évaluer si l’ordre dans lequel les employés complètent un exercice de test est lié au nombre de mois qu’ils ont été employés.

Dois-je utiliser la corrélation de Spearman ou de Pearson ?

La différence entre la corrélation Pearson et la corrélation Spearman est que la Pearson est plus appropriée pour les mesures prises à partir d’une échelle d’intervalle, tandis que la Spearman est plus appropriée pour les mesures prises à partir d’échelles ordinales.

Comment tester la corrélation ?

s=√SSEn-2 s = S S E n – 2 La variable ρ (rho) est le coefficient de corrélation de la population. Pour tester l’hypothèse nulle H : ρ = valeur hypothétique, utilisez un t- test de régression linéaire. L’hypothèse nulle la plus courante est H : ρ = 0 qui indique qu’il n’y a pas de relation linéaire entre x et y dans la population.

Comment déterminer s’il existe une corrélation entre deux variables ?

Pour calculer la corrélation , il faut d’abord déterminer la covariance des deux variables en question. Ensuite, il faut calculer l’écart-type de chaque variable . Le coefficient de corrélation est déterminé en divisant la covariance par le produit des écarts types des deux variables .

Quels sont les 5 types de corrélation ?

Types de corrélation

• Corrélation positive. La corrélation positive se produit lorsqu’une augmentation d’une variable augmente la valeur d’une autre.
• Corrélation négative. La corrélation négative se produit lorsqu’une augmentation d’une variable diminue la valeur d’une autre.
• Pas de corrélation.
• Corrélation parfaite.
• Corrélation forte.
• Corrélation faible.

.
A quoi sert la corrélation de Pearson ?

Coefficient de corrélation de Pearson . La corrélation est une technique permettant d’étudier la relation entre deux variables quantitatives et continues, par exemple l’âge et la pression artérielle. Aux seules fins de la corrélation , l’axe sur lequel les variables sont tracées n’a pas vraiment d’importance.

Pourquoi utilise-t-on la corrélation de Pearson ?

Utilisations communes La corrélation bivariée de Pearson indique ce qui suit : L’existence d’une relation linéaire statistiquement significative entre deux variables continues. La force d’une relation linéaire (c’est-à-dire à quel point la relation est proche d’être une ligne parfaitement droite).

Quels sont les types de corrélation ?

Types de corrélation

• Corrélation positive – lorsque la valeur d’une variable augmente par rapport à une autre.
• Corrélation négative – lorsque la valeur d’une variable diminue par rapport à une autre.
• Aucune corrélation – lorsqu’il n’y a pas de dépendance linéaire ou de relation entre les deux variables.

Comment classe-t-on les données ?

Le classement des données consiste à mettre les valeurs dans un ordre numérique, puis à attribuer de nouvelles valeurs pour indiquer où elles se situent dans l’ensemble ordonné. On donne à la plus petite valeur le numéro 1, à la plus grande valeur suivante le numéro 2, à la plus grande valeur suivante le numéro 3, etc.

.
Qu’entendez-vous par corrélation de rang ?

En statistique, une corrélation de rang est l’une de plusieurs statistiques qui mesurent une association ordinale-la relation entre les rangs de différentes variables ordinales ou différents rangs de la même variable, où un ‘ rang ‘ est l’affectation des étiquettes d’ordre ‘premier’, ‘deuxième’, ‘troisième’, etc. à différents

.
Que signifie le rho de Spearman ?

Le Rho de Spearman est un test non paramétrique utilisé pour mesurer la force de l’association entre deux variables, où la valeur r = 1 signifie une corrélation positive parfaite et la valeur r = -1 signifie une corrélation négative parfaite.

Qu’est-ce que r en statistique ?

En statistique , le coefficient de corrélation r mesure la force et la direction d’une relation linéaire entre deux variables sur un nuage de points. La valeur de r est toujours comprise entre +1 et -1.

Comment calcule-t-on Rho ?

Calcul de Rho et Rho en pratique La formule exacte de rho est compliquée. Mais elle est calculée comme la dérivée première de la valeur de l’option par rapport au taux sans risque. Rho mesure la variation attendue du prix d’une option pour une variation de 1 % du taux sans risque d’un bon du Trésor américain.

Que représente la valeur p dans la corrélation de Spearman ?

La p (ou probabilité) valeur obtenue par la calculatrice est une mesure de la probabilité ou de la vraisemblance que toute corrélation observée soit due au hasard. Les P – valeurs sont comprises entre 0 (0%) et 1 (100%). Une p – valeur proche de 1 suggère l’absence de corrélation autre que due au hasard et que votre hypothèse nulle est correcte.

Comment interpréter les coefficients phi ?

Interprétation du coefficient Phi La plage est de -1 à 1, où : 0 est une absence de relation. 1 est une relation positive parfaite : la plupart de vos données tombent le long des cellules diagonales. -1 est une relation négative parfaite : la plupart de vos données ne se trouvent pas sur la diagonale.

Que signifie la corrélation ?

La corrélation est une mesure statistique qui indique dans quelle mesure deux variables ou plus fluctuent ensemble. Une corrélation positive indique la mesure dans laquelle ces variables augmentent ou diminuent parallèlement ; une corrélation négative indique la mesure dans laquelle une variable augmente alors que l’autre diminue.

Que nous dit le coefficient de détermination ?

Le coefficient de détermination est utilisé pour expliquer dans quelle mesure la variabilité d’un facteur peut être causée par sa relation avec un autre facteur. Le coefficient de détermination est le carré du coefficient de corrélation , également connu sous le nom de  » R « , ce qui lui permet d’afficher le degré de corrélation linéaire entre deux variables.