Qu’est-ce que la fonction de distribution cumulative normale inverse ?

La inverse de la CDF (c’est-à-dire la fonction inverse ) vous indique quelle valeur x (dans cet exemple, le score z) ferait que F(x)-la distribution normale dans ce cas- renvoie une probabilité particulière p. En notation, c’est : F^–1(p) = x. Pour résumer : CDF = quelle zone/probabilité correspond à un z-score connu ?

De même, quel est l’inverse de la distribution cumulative normale standard ?

x = norminv( p ) renvoie l’ inverse de la fonction de distribution cumulative normale standard (cdf), évaluée aux valeurs de probabilité dans p . x = norminv( p , mu ) renvoie la inverse de la cdf normale avec la moyenne mu et l’écart standard unitaire, évaluée aux valeurs de probabilité en p .

Deuxièmement, qu’est-ce que la distribution inverse ? En théorie des probabilités et en statistique, une distribution inverse est la distribution de la réciproque d’une variable aléatoire. Dans l’algèbre des variables aléatoires, les distributions inverses sont des cas particuliers de la classe des distributions de rapport , dans laquelle la variable aléatoire numératrice a une distribution dégénérée.

A savoir également, que vous dit une fonction de distribution cumulative ?

La fonction de distribution cumulative (CDF) calcule la probabilité cumulative pour une valeur x donnée. Utilisez la FCD pour déterminer la probabilité qu’une observation aléatoire qui est prise dans la population soit inférieure ou égale à une certaine valeur.

Qu’est-ce que la fonction de distribution cumulative avec exemple ?

La fonction de distribution cumulative (FX) donne la probabilité que la variable aléatoire X soit inférieure ou égale à une certaine quantité x. Sa formule est la suivante : En additionnant les valeurs de toutes les issues inférieures ou égales à x, on obtient la solution.

Comment trouver la distribution cumulative ?

La fonction de distribution cumulative (CDF) de la variable aléatoire X est définie comme FX(x)=P(X≤x), pour tout x∈R.

Solution

1. Pour trouver la CDF, on note que.
2. Pour trouver P(2<X≤5), on peut écrire P(2<X≤5)=FX(5)-FX(2)=3132-34=732.
3. Pour trouver P(X>4), on peut écrire P(X>4)=1-P(X≤4)=1-FX(4)=1-1516=116.

Quand utiliseriez-vous la distribution exponentielle ?

La distribution exponentielle est l’une des distributions continues les plus utilisées. Elle est souvent utilisée pour modéliser le temps écoulé entre deux événements. Nous allons maintenant définir mathématiquement la distribution exponentielle , et en déduire sa moyenne et sa valeur espérée.

Qu’est-ce que l’inverse d’une fonction ?

En mathématiques, une fonction inverse (ou anti- fonction ) est une fonction qui « inverse » une autre fonction : si la fonction f appliquée à une entrée x donne un résultat de y, alors l’application de sa fonction inverse g à y donne le résultat x, et vice versa, c’est-à-dire , f(x) = y si et seulement si g(y) = x.

Qu’est-ce que le quantile d’une distribution ?

Les quantiles sont des points dans une distribution qui se rapportent à l’ordre de classement des valeurs dans cette distribution . Pour un échantillon, vous pouvez trouver n’importe quel quantile en triant l’échantillon. La valeur médiane de l’échantillon trié ( quantile moyen, 50e percentile ) est appelée médiane. Les limites sont les valeurs minimales et maximales.

Qu’est-ce que la fonction de densité de probabilité en statistique ?

La fonction de densité de probabilité ( PDF ) est une expression statistique qui définit une distribution de probabilité (la probabilité d’un résultat) pour une variable aléatoire discrète (par exemple, une action ou un ETF) par opposition à une variable aléatoire continue.

Qu’est-ce que la fonction de point de pourcentage ?

Fonction de point de pourcentage . La fonction de point de pourcentage (ppf) est l’inverse de la fonction de distribution cumulative . Pour cette raison, la fonction de point de pourcentage est aussi communément appelée la distribution inverse fonction .

Qu’est-ce que la probabilité cumulative ?

Une probabilité cumulative désigne la probabilité que la valeur d’une variable aléatoire se situe dans une plage spécifiée. Fréquemment, les probabilités cumulatives font référence à la probabilité qu’une variable aléatoire soit inférieure ou égale à une valeur spécifiée.

Que calcule Normsinv dans Excel ?

NORMSINV . Définition de NORMSINV : Un logiciel de Microsoft Excel .
qui fournit l’inverse de la distribution normale standarisée cumulée. Vous entrez la « probabilité qu’une valeur Z soit inférieure ou égale à… » et elle vous renvoie cette valeur Z (en termes de « sigmas », car il s’agit de la distribution normalisée de moyenne 0 et de sigma 1).

Comment trouver la probabilité inverse ?

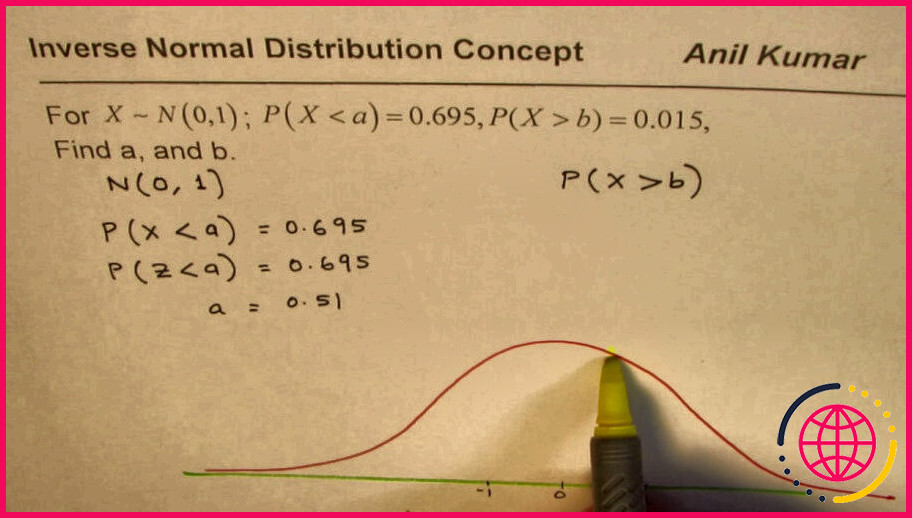
Ainsi, on demande la valeur de X qui donnera une aire sous la courbe égale à 0,023. C’est la valeur de la probabilité normale inverse. On peut l’écrire sous la forme P(X &lt ; a) = 0,023.

Détermination des valeurs de probabilité normale inverse

1. P = 0,0233 pour Z = -1,99.
2. P = 0,0228 pour Z = -2,00.
3. P = 0,0222 pour Z = -2,01.

Que signifie une distribution uniforme ?

Qu’est-ce que la distribution uniforme ? En statistique, un type de distribution de probabilité distribution dans laquelle toutes les issues sont également probables ; chaque variable a la même probabilité d’être l’issue. Une pièce de monnaie a également une distribution uniforme car la probabilité d’obtenir soit pile soit face lors d’un lancer de pièce est la même.

Qu’est-ce que la fonction de distribution cumulative normale standard ?

La fonction de distribution ( cumulative ) d’une variable aléatoire X, évaluée en x, est la probabilité que X prenne une valeur inférieure ou égale à x. Il suffit de laisser la moyenne et la variance de votre variable aléatoire à 0 et 1, respectivement. Cela s’appelle normaliser la distribution normale .

Qu’est-ce que la fonction de distribution cumulative en statistique ?

En théorie des probabilités et en statistique , la fonction de distribution cumulative ( CDF ) d’une variable aléatoire à valeur réelle , ou simplement fonction de distribution de , évaluée à , est la probabilité que prendra une valeur inférieure ou égale à ,

Quelle est la différence entre la fonction de densité de probabilité et la fonction de distribution cumulative ?

La Différence entre la PDF et la CDF : Cela signifie que la PDF s’intéresse à un point fixe ou à un intervalle alors que la CDF s’intéresse à tout ce qui est en dessous d’un point. La CDF est l’intégrale de PDF, donc PDF est la dérivée de CDF .

Pourquoi la CDF est continue droite ?

La fonction de distribution F est continue droite en un point a si et seulement si pour toute suite décroissante de nombres réels xnn≥1 telle que xn↓a on a F(xn)↓F(a).

Qu’est-ce que la fonction de distribution cumulative complémentaire ?

La fonction de distribution cumulative complémentaire comme son nom l’indique complète la fonction de distribution cumulative (CDF). La CDF est utilisée pour trouver la probabilité qu’une variable prenne une valeur inférieure ou égale à x, la CCDF est utilisée pour trouver la probabilité qu’une variable prenne une valeur supérieure à x.

Que signifie la distribution de probabilité ?

Une distribution de probabilité est une fonction statistique qui décrit toutes les valeurs et probabilités possibles qu’une variable aléatoire peut prendre dans un intervalle donné. Ces facteurs comprennent la moyenne (moyenne), l’écart-type, l’asymétrie et l’aplatissement de la distribution.

Que signifie la fonction de densité cumulative ?

Définition de la fonction de distribution cumulative : une fonction qui donne la probabilité qu’une variable aléatoire soit inférieure ou égale à la variable indépendante de la fonction .