Qu’est-ce qu’un CAN (convertisseur analogique-numérique) et comment fonctionne-t-il ?

Principaux enseignements

• Les convertisseurs analogiques-numériques sont largement utilisés pour convertir des signaux analogiques, tels que le son et la lumière, en valeurs numériques qui peuvent être utilisées dans diverses applications.
• Le taux d’échantillonnage d’un CAN détermine le nombre de lectures effectuées par seconde, des taux d’échantillonnage plus élevés permettant une représentation plus précise du signal.
• Le débit binaire d’un CAN affecte la qualité de l’échantillon obtenu, un plus grand nombre de bits se traduisant par des mesures plus fluides et plus précises. Les différents types de CAN offrent des compromis différents en termes de vitesse, de précision et de consommation d’énergie.

Les convertisseurs analogique-numérique (CAN) sont incroyablement utiles pour transformer les phénomènes du monde réel en valeurs utilisables dans les projets de programmation. Mais comment un convertisseur analogique-numérique peut-il convertir des signaux analogiques en signaux numériques utilisables partout ?

À quoi servent les CAN ?

Vous trouverez des CAN un peu partout. Ils sont dans votre téléphone, convertissant votre voix en une chaîne de valeurs binaires. Dans votre voiture, ils mesurent la rotation des roues. Ils sont dans les oscilloscopes, aidant à capturer les signaux et à les représenter. Pourtant, la plupart des gens les auront utilisés dans le monde de la vidéo et de l’audio, où il est fondamental de faire entrer la lumière et le son dans un espace numérique.

Qu’est-ce qu’une fréquence d’échantillonnage ? Comment la fréquence d’échantillonnage affecte-t-elle un CAN ?

L’une des mesures les plus critiques d’un CAN est le taux d’échantillonnage : le nombre de lectures effectuées chaque seconde.

Un oscilloscope très haut de gamme peut prendre dix milliards d’échantillons par seconde. Le petit CAN MCP3008 peut en prendre deux cent mille, ce qui est relativement modeste. Dans le monde audio, une fréquence d’échantillonnage de 44 100 par seconde (44,1 kHz) est typique.

Plus nous prenons d’échantillons, plus nous pouvons représenter un signal avec précision. Parfois, c’est essentiel, parfois non. Supposons que nous construisions une banque de faders (conçue pour contrôler l’électronique, comme celle que l’on trouve sur un pupitre d’éclairage ou d’audio) avec quelques douzaines de potentiomètres. Dans ce cas, il est peu probable que les valeurs que nous devons mesurer changent des millions de fois par seconde, car nos doigts ne peuvent pas se déplacer aussi rapidement. Nous avons juste besoin d’un nombre suffisant d’échantillons pour que le résultat soit fluide et réactif.

Qu’est-ce que le débit binaire ? Le débit binaire affecte-t-il la qualité d’un CAN ?

Nous devons également réfléchir à la qualité de l’échantillon que nous obtenons. Celle-ci est largement déterminée par le débit binaire, qui nous indique le nombre d’états on-off que nous pouvons utiliser pour représenter numériquement la tension. Plus nous avons de bits, plus nous pouvons enregistrer de valeurs possibles dans un échantillon donné et plus le résultat final est lisse et précis.

Nous avons déjà écrit sur le système binaire et son fonctionnement. Si vous n’êtes pas sûr de vous, c’est un bon point de départ. De combien de bits avons-nous besoin ? Là encore, cela dépend de ce que nous essayons d’accomplir. Parfois, nous sommes limités par le protocole que nous utilisons. Par exemple, le protocole MIDI 1.0 est limité à des valeurs de sept bits (et parfois de quatorze bits). Dans d’autres cas, le facteur limitant peut être la perception humaine. Si l’augmentation de la fidélité ne produit pas d’amélioration perceptible du résultat, cela n’en vaut peut-être pas la peine.

Comment le multiplexage améliore-t-il la qualité du CAN ?

Les puces ADC les plus répandues, telles que le ADS1115 et le MCP3008 offrent de nombreuses entrées. Mais sous le capot, ils ne contiennent en réalité qu’un seul ADC. Cela est possible grâce aux multiplexeurs intégrés dans ces appareils. Les multiplexeurs sont omniprésents dans le monde de l’électronique et des télécommunications. Ce sont des commutateurs numériques qui contrôlent le trafic de votre CAN. Le CAN peut échantillonner un canal, puis le suivant, puis le suivant. Ainsi, si vous disposez de huit canaux et d’une fréquence d’échantillonnage de 200 000, vous pouvez passer d’un canal à l’autre en prenant 25 000 échantillons par canal.

Quels sont les types de CAN ?

Les CAN fonctionnent de différentes manières, en fonction du coût et des capacités requises.

A ADC Flash fonctionne par l’intermédiaire d’un diviseur de tension très complexe. Une banque de résistances divise la tension de référence en incréments, qui sont ensuite testés par rapport à l’entrée via une banque de comparateurs. Les CAN flash sont rapides comme l’éclair, mais ils sont limités en termes de profondeur de bits en raison du nombre de comparateurs requis. Ils sont également gourmands en énergie pour la même raison.

A Sous-calculateur analogique cherche à compenser ces faiblesses en répartissant le travail entre deux unités distinctes : l’une pour calculer grossièrement la tension et l’autre pour la calculer précisément. En divisant le travail, nous pouvons réduire le nombre de comparateurs. Certains CDA de sous-catégorie divisent le travail en trois étapes, avec une correction d’erreur intégrée en cours de route.

SAR (Registre d’approximation successive) Les CAN effectuent leur travail par le biais d’une sorte de recherche binaire. Supposons que nous ayons huit bits à remplir. Le SAR commencera à partir de 10000000, qui est la valeur moyenne (00000000 étant la valeur inférieure et 11111111 la valeur supérieure). Si la tension dépasse ce point central, le SAR conservera le chiffre le plus à gauche à 1 ; dans le cas contraire, le SAR mettra le chiffre le plus à gauche à 0. Nous pouvons répéter le processus avec le chiffre suivant et ainsi de suite de manière récursive. Ainsi, la valeur supposée se rapprochera progressivement de la valeur réelle :

De cette manière, nous réduisons continuellement la recherche, en divisant les possibilités en deux et en demandant si le résultat est supérieur ou inférieur au point médian. Dans le cas présent, la valeur se situe quelque part entre 0 et 255 ; après quelques itérations, l’ADC a déterminé qu’elle se situait autour de 77.

Sigma-delta sont probablement les plus difficiles à comprendre. Ils sont utilisés pour des applications musicales et de mesure de signaux de haute précision. Ils fonctionnent en suréchantillonnant un signal et en affinant le résultat à l’aide d’un filtrage et de mathématiques extrêmement complexes. Ce processus réduit effectivement la fréquence d’échantillonnage tout en augmentant la précision. Ces CAN sont parfaits lorsque le bruit et la précision sont plus importants que la vitesse.

Enfin, nous avons Intégration des CAN qui sont encore plus lents que les convertisseurs sigma-delta. Ils fonctionnent à l’aide d’un condensateur, dont le taux de charge peut être utilisé pour déterminer la tension d’entrée. La fréquence d’échantillonnage est souvent synchronisée avec la fréquence de l’alimentation, ce qui permet de réduire le bruit au minimum.

Qu’est-ce que la théorie de Nyquist-Shannon ?

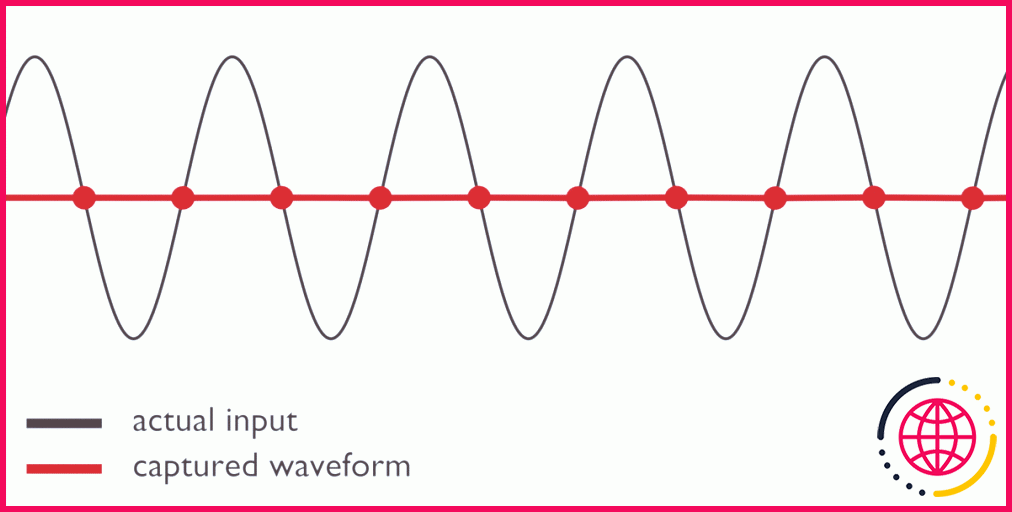
Supposons que nous voulions décrire numériquement un signal analogique. Pour ce faire, nous avons besoin d’au moins deux points pour chaque cycle donné : un en haut et un en bas. Par conséquent, notre fréquence d’échantillonnage doit être au moins deux fois supérieure à la fréquence la plus élevée que nous prévoyons de mesurer.

C’est ce qu’on appelle la fréquence de Nyquist, d’après le physicien américano-suédois Harry Nyquist. La théorie porte le nom de Nyquist et de Claude Shannon (mathématicien et cryptographe de premier plan), mais pas celui d’Edmund Whittaker, qui a eu l’idée avant eux.

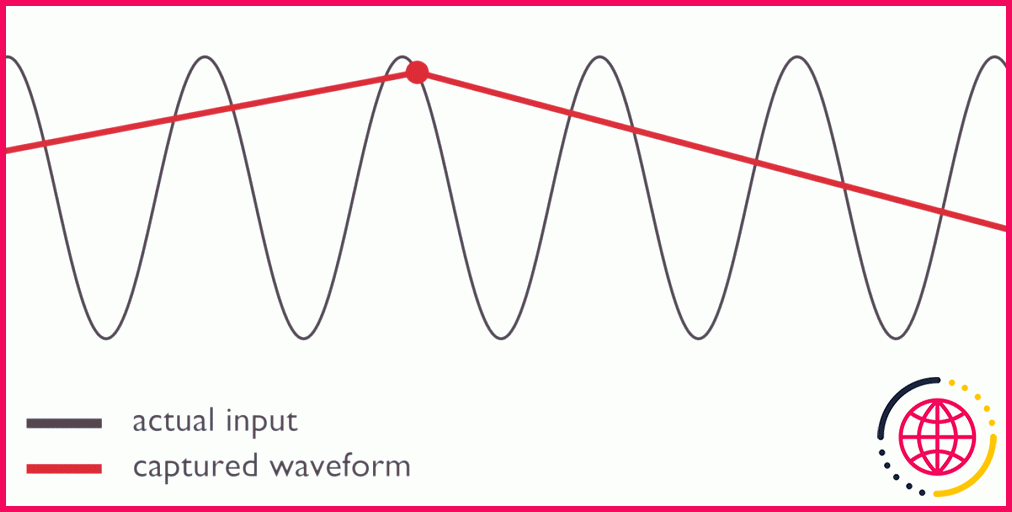
Quel que soit l’auteur de la théorie, celle-ci pose un problème. Il est impossible de savoir à l’avance quand le haut et le bas d’une forme d’onde arriveront. Et si nous prenions nos échantillons à mi-chemin de la forme d’onde entrante ? Observez comment un décalage dans le signal entrant peut aplatir complètement notre résultat capturé :

Ou même halluciner de nouvelles formes d’onde qui n’existaient pas auparavant :

Ces hallucinations sont connues sous le nom de alias.

Le problème de l’alias

Vous connaissez probablement l’illusion de la « roue de chariot » qui se produit parfois lorsqu’un objet en rotation est filmé. Les roues d’une voiture ou les pales d’un hélicoptère semblent tourner vers l’arrière, mais très lentement. Dans certains cas, les pales peuvent s’arrêter complètement (avec des résultats franchement étranges – regardez la vidéo ci-dessous !)

En jouant à un jeu vidéo plus ancien, vous avez peut-être remarqué que les lignes parallèles produisent parfois d’étranges artefacts de déformation. Les clôtures, les escaliers et les sauteurs à rayures prennent alors un aspect très particulier. Et que dire de ces étranges sifflements que l’on entend parfois en écoutant quelqu’un parler sur une connexion numérique de mauvaise qualité ? Il s’agit de distorsion, mais d’un type particulier de distorsion. Qu’en est-il de toutes ces fréquences hideuses qui émergent du bruit ? Si vous écoutez un contenu riche en harmoniques, comme une batterie, l’effet est encore plus évident, surtout dans les aigus.

Si vous comprenez la cause de l’un de ces phénomènes, vous êtes sur la bonne voie pour les comprendre tous. Dans le cas de la roue de chariot, la fréquence d’images fixe signifie que nous ne pouvons pas capturer le mouvement correctement. Si quelque chose tourne de 350° à chaque image, il est naturel de percevoir qu’il a en fait reculé de 10°. En d’autres termes, il n’y a pas assez d’informations pour représenter fidèlement ce qui se passe. Les échantillons que nous prélevons sont mal alignés avec ce que nous essayons de mesurer.

Ce problème n’est pas propre à la conversion analogique-numérique. Dans de nombreux cas, nous convertissons un type de signal numérique en un autre.

Quelle est donc la solution ? Il y en a plusieurs. Nous pourrions appliquer un filtre spécial pour traiter ces artefacts, ce que font de nombreux CDA sous le capot. Ou bien nous pouvons prendre beaucoup, beaucoup plus d’échantillons qu’il n’en faut. Plus nous prenons d’échantillons, plus notre image de l’onde devient précise :

Échantillonner avec une plus grande qualité pour obtenir les meilleurs résultats

Si ce genre de choses vous intéresse, la bonne nouvelle est que nous n’avons fait qu’effleurer ce sujet. Il y a des profondeurs à sonder ici : Les CAN sont extrêmement complexes.

Mais du point de vue de l’utilisateur final ou de l’amateur moyen d’Arduino, ils sont également très simples. Des tensions entrent et des nombres sortent. Ainsi, quel que soit l’objet que vous cherchez à mesurer – qu’il s’agisse du taux d’humidité d’une parcelle de terre, des oscillations d’une boîte vocale humaine ou d’un flux de photons se réfractant à travers une lentille – il y a de fortes chances qu’il existe un CAN qui fasse l’affaire.

Améliorez votre QI technologique grâce à nos lettres d’information gratuites

En vous abonnant, vous acceptez notre politique de confidentialité et pouvez recevoir des communications occasionnelles ; vous pouvez vous désabonner à tout moment.