Comment calculer les combinaisons ?

En mathématiques, une combinaison est une sélection d’éléments d’un ensemble, où l’ordre de sélection n’a pas d’importance. Par exemple, étant donné trois fruits, disons des pommes, des oranges et des bananes, trois combinaisons de deux peuvent être tirées de cet ensemble : une pomme et une orange ; une pomme et une banane; ou une orange et une banane. Plus formellement, une k-combinaison d’un ensemble S est tout sous-ensemble de k éléments distincts de S. Si l’ensemble a n éléments, le nombre de k-combinaisons est égal au coefficient binomial.

La définition ci-dessus commence par une indexation basée sur 0. Autrement dit, le zéroième élément de S est considéré comme distinct du premier élément de S, et ainsi de suite. En tant que tel, il existe n + 1 k-combinaisons lorsque l’on considère un ensemble à n éléments. Lorsque l’indexation basée sur 1 est utilisée à la place (comme c’est plus courant dans l’énumération combinatoire), la formule ci-dessus pour le nombre de k-combinaisons devient.

Le fait que les combinaisons ne sont pas affectées par l’ordre peut être représenté mathématiquement en disant que deux combinaisons sont considérées comme égales si elles ont le même multi-ensemble d’éléments. En d’autres termes, si nous considérons que deux combinaisons ne sont différentes que si elles ont des ordres d’éléments différents (c’est-à-dire des séquences différentes), alors nous comptons des k-séquences plutôt que des k-combinaisons.[1] Par exemple, étant donné trois fruits comme précédemment : des pommes, des oranges et des bananes, il y a six séquences 2 différentes qui peuvent être tirées de cet ensemble : {pomme, orange}, {pomme, banane}, {orange, pomme}, {orange banane }, {pomme banane} et {orange banane} mais seulement trois 2-combinaisons différentes puisque {pomme orange} = {pomme orange}. Le nombre de 2-séquences que l’on peut tirer d’un ensemble à n éléments est donc égal à n(n − 1), tandis que le nombre de 2-combinaisons est donné par .

Pour calculer des combinaisons en Python, nous pouvons utiliser itertools.combinations(). Cette fonction prend deux paramètres, le premier étant l’objet itérable à partir duquel nous voulons obtenir des combinaisons (dans notre cas, une liste) et le second étant le nombre d’éléments que nous voulons dans chaque combinaison (2 dans notre cas). Donc, si nous avons une liste [1, 2, 3] et nous voulons toutes les combinaisons possibles de 2 éléments que nous ferions :

>>> importer itertools.

>>> liste(itertools.combinations([1, 2, 3]2)).

[(1, 2), (1 3), (2 3)]

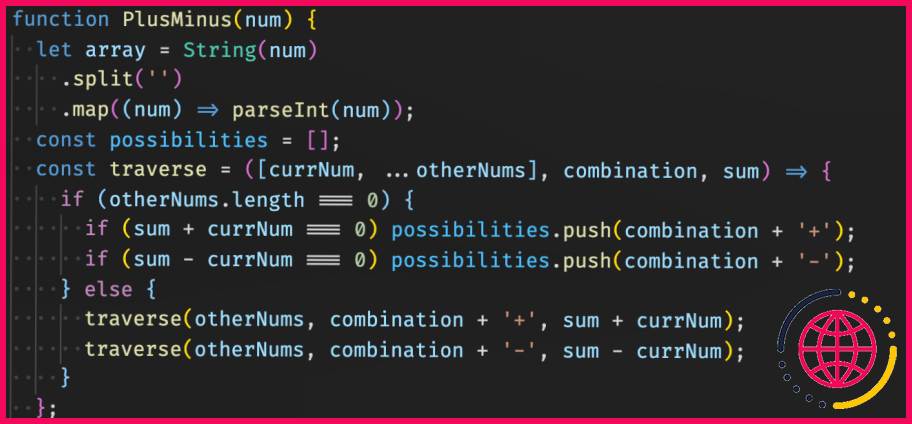
Une autre façon de calculer des combinaisons serait d’utiliser la récursivité. Nous pouvons définir une fonction récursive combo() qui prend dans notre liste L ainsi que le nombre d’éléments que nous voulons dans chaque combinaison k. Le cas de base de notre fonction se produit lorsque L n’a plus d’éléments ou lorsque k est égal à 0 – dans les deux cas, nous renvoyons simplement une liste vide car il n’y a pas de combinaisons possibles. Sinon, ce que nous voulons faire est de parcourir chaque élément de L en l’ajoutant à tous les combos possibles renvoyés par combo(L[i+1:],k-1). Nous devons également nous assurer que lors de l’ajout de chaque élément aux combos qui ont déjà été renvoyés par notre fonction, nous créons de nouvelles listes – de cette façon, chaque combo n’est ajouté qu’une seule fois plutôt que de créer des doublons.[2] Voir ci-dessous le code implémentant cette approche :

Rappelons que les combinaisons sont un moyen de calculer le total des résultats d’un événement où l’ordre des résultats n’a pas d’importance. Pour calculer les combinaisons, nous utiliserons la formule nCr = n ! / r ! * (n – r) !, où n représente le nombre d’éléments, et r représente le nombre d’éléments choisis à un moment donné.

Existe-t-il une formule pour les combinaisons ?

La formule des combinaisons est : nCr = n ! / ((n – r) ! r !) n = le nombre d’articles.

Combien de combinaisons de 12 chiffres y a-t-il ?

x2x1=479001600. Ce nombre est appelé « douze factoriel » et s’écrit 12!donc, par exemple 4!= 4x3x2x1=24. Ces 479001600 « chaînes » des 12 nombres, par exemple 1,2,3,4,5,6,7,8,9,10,11,12 et 2,4,6,8,10,12,11,9,7,5,3,1, les mathématiciens les appellent des permutations des 12 nombres plutôt que des combinaisons.

Comment faire la liste de toutes les combinaisons possibles ?

Pour créer la liste de toutes les combinaisons possibles :

1. Cliquez sur le bouton Développer dans l’en-tête de la colonne. Dans le sous-menu : Sélectionnez uniquement la colonne contenant les données que nous souhaitons conserver (c’est-à-dire, dans notre exemple, décochez la colonne Temp) .
2. La liste des combinaisons possibles apparaît maintenant dans la fenêtre Power Query.

Quelle est la formule pour les combinaisons et les permutations ?

Quelle est la formule des permutations et des combinaisons ? La formule pour les permutations est : nPr = n!/(n-r) ! La formule pour les combinaisons est : nCr = n!/[r !

Combien de combinaisons des nombres 1 2 3 4 y a-t-il ?

Explication : Si nous regardons le nombre de nombres que nous pouvons créer en utilisant les nombres 1, 2, 3 et 4, nous pouvons le calculer de la façon suivante : pour chaque chiffre (milliers, centaines, dizaines, uns), nous avons 4 choix de nombres. Et donc nous pouvons créer 4×4×4×4=44=256 nombres.

Combien de combinaisons de 4 y a-t-il ?

Quelles sont les combinaisons possibles de 4 nombres ? Il y a 5 040 combinaisons de 4 chiffres lorsque les chiffres ne sont utilisés qu’une seule fois.

Combien de combinaisons possibles y a-t-il pour un code à 4 chiffres ?

Il existe 10 000 combinaisons possibles dans lesquelles les chiffres de 0 à 9 peuvent être disposés pour former un code à quatre chiffres. Berry les a analysées pour trouver lesquelles sont les moins et les plus prévisibles.

Combien de combinaisons de 7 chiffres y a-t-il ?

Le nombre de combinaisons possibles avec 7 chiffres est de 127.

Quel est l’exemple de combinaison ?

Une combinaison est une sélection de tout ou partie d’un ensemble d’objets, sans tenir compte de l’ordre dans lequel les objets sont sélectionnés. Par exemple, supposons que nous ayons un ensemble de trois lettres : A, B et C. On peut se demander de combien de façons on peut sélectionner 2 lettres dans cet ensemble. Chaque sélection possible serait un exemple de combinaison.

Comment calcule-t-on les permutations ?

Pour calculer le nombre de permutations, prenez le nombre de possibilités pour chaque événement, puis multipliez ce nombre par lui-même X fois, où X est égal au nombre d’événements dans la séquence. Par exemple, avec les codes PIN à quatre chiffres, chaque chiffre peut aller de 0 à 9, ce qui nous donne 10 possibilités pour chaque chiffre.

Combien de combinaisons de 10 chiffres y a-t-il ?

Le nombre de combinaisons possibles avec 10 chiffres est de 1 023.

Comment calcule-t-on la formule n ?

Utiliser la formule t _n = a + (n – 1) d pour résoudre n. Introduisez le dernier terme (t _n), le premier terme (a) et la différence commune (d). Travaillez sur l’équation jusqu’à ce que vous ayez résolu n. Par exemple, commencez par écrire : -61 = 107 + (n – 1) -6.

Quelle est la formule pour nPr ?

Permutation : nPr représente la probabilité de sélectionner un ensemble ordonné de  » r  » objets dans un groupe de  » n  » nombre d’objets. L’ordre des objets a de l’importance en cas de permutation. La formule pour trouver nPr est donnée par : nPr = n!/(n-r) !

Combien de combinaisons de 3 objets y a-t-il ?

3*3*3=27 possibilités uniques.

Qu’est-ce qu’une combinaison et sa formule ?

Formule de combinaison. La formule de combinaison est utilisée pour trouver le nombre de façons de sélectionner des éléments dans une collection, de telle sorte que l’ordre de sélection n’a pas d’importance. En termes simples, la combinaison consiste à sélectionner des objets ou des choses dans un groupe plus important où l’ordre n’a pas d’importance.

Qu’est-ce qu’on appelle la combinaison ?

Une combinaison est une technique mathématique qui détermine le nombre d’arrangements possibles dans une collection d’éléments où l’ordre de la sélection n’a pas d’importance. Dans les combinaisons, on peut sélectionner les éléments dans n’importe quel ordre. Les combinaisons peuvent être confondues avec les permutations.

Quels sont les types de combinaison ?

Les réactions de combinaison sont de trois types :

• Dans le premier type de réaction de combinaison, un élément se combine avec un autre élément pour former un nouveau composé.
• Dans le deuxième type de réaction de combinaison, un élément se combine avec un composé.
• Dans le troisième type de combinaison, 2 ou plusieurs composés se combinent pour former un nouveau composé.

Comment appelle-t-on un nombre à 7 chiffres ?

Un nombre à 7 chiffres se lit comme des millions ou dix-lakhs. Maintenant, savez-vous combien de zéros il y a dans un million ? Voyons voir. 10 uns font une dizaine, 10 dizaines font une centaine, 10 centaines font un millier, 10 milliers font un dix-millier, 10 dix-milliers font un cent-millier et 10 cent-milliers font un million.

Combien de nombres uniques à 7 chiffres y a-t-il ?

Il y a 9000000 numéros à sept chiffres.