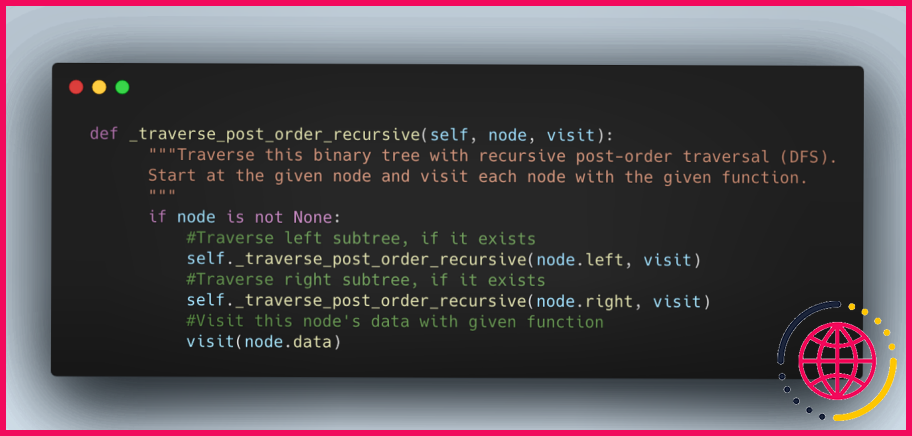
Quelle est l’utilité de la traversée d’un arbre binaire ?

La traversée d’arbre binaire est le processus de visite de chaque nœud dans un arbre binaire, en commençant par le nœud racine et en descendant les sous-arbres gauche et droit jusqu’à ce que tous les nœuds aient été visités. Il existe trois façons courantes de parcourir un arbre binaire : pré-ordre, dans l’ordre et post-ordre.

La traversée de pré-ordre visite d’abord le nœud racine, puis le sous-arbre gauche, puis le sous-arbre droit. Le parcours dans l’ordre visite d’abord le sous-arbre gauche, puis le nœud racine, puis le sous-arbre droit. La traversée post-ordre visite d’abord le sous-arbre gauche, puis le sous-arbre droit, puis le nœud racine.

La traversée d’arbre binaire est utilisée pour visiter tous les nœuds d’un arbre binaire afin de les traiter d’une manière ou d’une autre. Par exemple, le parcours de pré-ordre peut être utilisé pour créer une copie d’un arbre binaire. Le parcours dans l’ordre peut être utilisé pour imprimer toutes les valeurs d’un arbre binaire dans un ordre trié. La traversée post-ordre peut être utilisée pour supprimer tous les nœuds d’un arbre binaire.

Souvent, nous souhaitons traiter un arbre binaire en « visitant » chacun de ses nœuds, en effectuant à chaque fois une action spécifique comme l’impression du contenu du nœud. Tout processus permettant de visiter tous les nœuds dans un certain ordre est appelé une traversée.

Quelle est l’utilité de la traversée d’un arbre ?

En informatique, la traversée d’arbre (également connue sous le nom de recherche d’arbre et de marche dans l’arbre) est une forme de traversée de graphe et se réfère au processus de visite (par exemple, la récupération, la mise à jour ou la suppression) de chaque nœud dans une structure de données en arbre, exactement une fois. Ces traversées sont classées selon l’ordre dans lequel les nœuds sont visités.

Pourquoi utilise-t-on l’arbre binaire ?

En informatique, les arbres binaires sont principalement utilisés pour la recherche et le tri car ils fournissent un moyen de stocker les données de manière hiérarchique. Certaines opérations courantes qui peuvent être effectuées sur les arbres binaires comprennent l’insertion, la suppression et la traversée.

Quelles sont les traversées d’arbres binaires expliquer avec exemple ?

Dans cette traversée, le nœud racine est visité en premier, puis son enfant gauche et ensuite son enfant droit. Ce traversal de pré-ordre est applicable pour chaque nœud racine de tous les sous-arbres de l’arbre. Dans l’exemple ci-dessus d’arbre binaire, on visite d’abord le nœud racine ‘A’ puis son enfant gauche ‘B’ qui est une racine pour D et F.

Où peut-on utiliser l’arbre binaire ?

Applications des arbres binaires

• Arbre de recherche binaire – Utilisé dans de nombreuses applications de recherche qui montrent et cachent constamment des données, par exemple des données.
• Partition de l’espace binaire – Utilisé dans presque tous les jeux vidéo 3D pour déterminer quels objets doivent être rendus.
• Essais binaires – Utilisés dans presque tous les routeurs à large bande passante pour stocker les tables de routeur.

Combien d’arbres binaires sont possibles avec 10 nœuds ?

C’est 1014.

Qu’est-ce qu’un arbre parfait ?

Un arbre binaire parfait est un type d’arbre binaire dans lequel chaque nœud interne a exactement deux nœuds enfants et tous les nœuds feuilles sont au même niveau. Arbre binaire parfait. Tous les nœuds internes ont un degré de 2.

Quels sont les types de traversée d’un arbre binaire ?

Les algorithmes de traversée d’arbre peuvent être classés globalement en deux catégories :

• Algorithmes de recherche en profondeur et en premier (DFS).
• Algorithmes de recherche en largeur et en premier (BFS).

Qu’entendez-vous par traversée d’un arbre binaire ?

Traversée de l’arbre binaire. La traversée d’un arbre est le processus qui consiste à visiter chaque nœud de l’arbre exactement une fois. La visite de chaque nœud d’un graphe doit se faire de manière systématique. Si la recherche aboutit à la visite de tous les sommets, elle est appelée une traversée.

Quel est l’exemple de traversée en ordre ?

Exemple de traversée en ordre

nous commençons l’appel récursif à partir de 30(racine) puis nous nous déplaçons vers 20 (20 ont aussi des sous-arbres donc appliquer en ordre sur lui),15 et 5. 5 n’a pas d’enfant . donc imprimer 5 puis se déplacer vers son nœud parent qui est 15 imprimer et ensuite se déplacer vers le nœud droit de 15 qui est 18. maintenant traverser récursivement vers le sous-arbre droit du nœud racine .

Quels sont les avantages de l’arbre de recherche binaire ?

Avantages des arbres binaires.

• Un moyen idéal pour aller avec la manière hiérarchique de stocker les données.
• Reflètent les relations structurelles qui existent dans l’ensemble de données donné.
• Rendent l’insertion et la suppression plus rapides que les listes et tableaux liés.
• Un moyen flexible de conserver et de déplacer des données.
• Sont utilisés pour stocker autant de nœuds que possible.

Qu’est-ce que la BST, donnez un exemple concret ?

Un arbre de recherche binaire auto-équilibré est utilisé pour maintenir un flux trié de données. Par exemple, supposons que nous recevons des commandes en ligne et que nous voulons maintenir les données en direct (dans la RAM) dans l’ordre trié des prix. Par exemple, nous souhaitons connaître le nombre d’articles achetés à un coût inférieur à un coût donné à tout moment.

Pourquoi avons-nous besoin d’un arbre binaire qui est équilibré en hauteur ?

2. Pourquoi avons-nous besoin d’un arbre binaire qui est équilibré en hauteur ? Explication : Dans le monde réel, traiter des valeurs aléatoires n’est souvent pas possible, la probabilité que u traite des valeurs non aléatoires(comme séquentiel) conduit à la plupart des arbres skew, ce qui conduit au pire cas. donc nous faisons l’équilibre de hauteur par des rotations.

Quelle est la bonne façon de poster un arbre ordonné ?

Traversée post ordonnée d’un arbre binaire en O(N) en utilisant un espace O(1).

1. Trouver l’enfant le plus à droite dans le sous-arbre de gauche.
2. Si l’enfant droit de l’enfant le plus à droite est NULL. Faire de current l’enfant droit du nœud le plus à droite. Traverser l’enfant gauche, current = current-.>gauche.
3. Sinon, mettez le pointeur droit de l’enfant le plus à droite à NULL.

Qu’est-ce que l’on entend par traversée ?

nom. action ou processus de passer à travers, sur, ou à travers:Un problème avec le vaisseau spatial Voyager 2 alors qu’il commençait sa traversée des anneaux de Saturne a finalement été lié à des collisions à grande vitesse avec des micrométéorites. Ordinateurs.

Qu’est-ce qu’un arbre binaire complet ?

Un arbre binaire complet est défini comme un arbre binaire dans lequel tous les nœuds ont soit zéro, soit deux nœuds enfants. Inversement, il n’y a aucun nœud dans un arbre binaire complet, qui a un nœud enfant.

Quelles sont les techniques de traversée ?

Dans le cas des arbres binaires enracinés, trois techniques de traversée récursive sont largement utilisées : Inorder Traversal. Preorder Traversal. Traversée post-ordre.

Quelle est la différence entre un arbre binaire plein et un arbre binaire complet ?

Arbres binaires complets v.s. Complete. Un arbre binaire complet (parfois arbre binaire propre ou 2-tree) est un arbre dans lequel chaque nœud autre que les feuilles a deux enfants. Un arbre binaire complet est un arbre binaire dans lequel chaque niveau, sauf éventuellement le dernier, est complètement rempli, et tous les nœuds sont aussi à gauche que possible.

Quel est l’exemple d’un arbre binaire ?

Un arbre binaire parfait est un arbre binaire dans lequel tous les nœuds intérieurs ont deux enfants et toutes les feuilles ont la même profondeur ou le même niveau. Un exemple d’arbre binaire parfait est le tableau d’ascendance (non incestueux) d’une personne à une profondeur donnée, car chaque personne a exactement deux parents biologiques (une mère et un père).

Combien de types d’arbres binaires existe-t-il ?

Voici chacun des types d’arbres binaires en détail :

• Arbre binaire complet. C’est un type particulier d’arbre binaire qui a soit zéro enfant, soit deux enfants.
• Arbre binaire complet.
• Arbre binaire parfait.
• Arbre binaire équilibré.
• Arbre binaire dégénéré.

Quelles sont les propriétés de l’arbre binaire ?

Intéressons-nous maintenant à quelques propriétés de base d’un arbre binaire :

• Un arbre binaire peut avoir un maximum de nœuds au niveau si le niveau de la racine est nul.
• Lorsque chaque nœud d’un arbre binaire a un ou deux enfants, le nombre de nœuds feuilles (nœuds sans enfants) est supérieur d’une unité au nombre de nœuds qui ont deux enfants.

Un arbre binaire peut-il avoir 1 enfant ?

Un arbre binaire est un arbre dans lequel aucun nœud n’a plus de deux enfants, et chaque enfant est soit un enfant gauche, soit un enfant droit, même s’il est le seul enfant de son parent. Un arbre binaire complet est un arbre dans lequel chaque nœud interne a deux enfants.

Combien de nœuds peut avoir un arbre ?

Si l’arbre binaire a une hauteur h, le nombre maximal de nœuds sera lorsque tous les niveaux seront complètement pleins. Le nombre total de nœuds sera de 2^0 + 2^1 + . 2^h = 2^(h+1)-1. Par exemple, l’arbre binaire représenté sur la figure 2(b) avec une hauteur de 2 a 2^(2+1)-1 = 7 nœuds.

Que signifie un arbre binaire parfait ?

(définition) Définition : Un arbre binaire dont tous les nœuds feuilles ont la même profondeur. Tous les nœuds internes ont un degré 2.

Combien d’arbres binaires complets sont possibles avec N nœuds ?

Le nombre d’arbres binaires complets avec n nœuds est donc C((n-1)/2).