Programmation dynamique : exemples, problèmes courants et solutions

Il ne fait aucun doute que les problèmes de programmes dynamiques peuvent être extrêmement intimidants lors d’un entretien de codage. Même si vous reconnaissez qu’un problème doit être résolu à l’aide d’une approche de programmes dynamiques, il est difficile de trouver une solution de travail en un minimum de temps.

La meilleure façon d’être doué pour les problèmes de programmation dynamiques est d’en traverser autant que possible. Bien que vous n’ayez pas nécessairement besoin de mémoriser l’option pour chaque problème, il est bon d’avoir une suggestion sur la façon exacte de gérer un problème.

Qu’est-ce que la programmation dynamique ?

En termes simples, les spectacles dynamiques sont une méthode d’optimisation pour les algorithmes récursifs, dont la majorité sont utilisés pour résoudre des problèmes informatiques ou mathématiques.

Vous pouvez également l’appeler une méthode mathématique pour résoudre un problème d’optimisation en le décomposant en sous-problèmes plus faciles. Un principe crucial sur lequel les spectacles dynamiques sont basés est que l’option idéale à un problème dépend des remèdes à ses sous-problèmes.

Partout où nous voyons un service récursif qui demande à plusieurs reprises les mêmes entrées, nous pouvons le maximiser en utilisant une programmation dynamique. La suggestion est de simplement conserver les résultats des sous-problèmes pour s’assurer que nous n’avons pas à les recalculer en cas de besoin plus tard.

Les services programmés dynamiquement ont une complexité polynomiale qui garantit un temps d’exécution beaucoup plus rapide que d’autres stratégies comme la récursivité ou le retour en arrière. Dans la plupart des cas, la programmation dynamique minimise les complexités temporelles, également appelées big-O, du rapide au polynomial.

Maintenant que vous avez une bonne idée de ce que sont les programmes dynamiques, il est temps de vérifier quelques problèmes courants et leurs options.

Problèmes de programmation dynamique

1. Problème de sac à dos

Énoncé du problème

Étant donné une collection de produits, chacun avec un poids ainsi qu’une valeur, établissez le nombre de chaque article à inclure dans une collection pour vous assurer que le poids total ne dépasse pas une limite donnée et que la valeur globale est aussi grande que réalisable.

On vous donne 2 plages d’entiers valeurs et aussi poids qui représentent des valeurs et des poids associés à n choses spécifiquement. Un entier est également fourni O qui représente la capacité du sac à dos.

Ici, nous résolvons le problème du sac à dos 0/1, qui indique que nous pouvons choisir d’ajouter un produit ou de l’exclure.

Algorithme

• Créez une plage bidimensionnelle avec n +1 rangées et w +1 Colonnes. Un numéro de ligne n signifie la collection de choses de 1 à je ainsi qu’un numéro de colonne w désigne la capacité maximale d’apport du sac.
• La valeur numérique à signifie la valeur totale des articles jusqu’à je dans un sac pouvant transporter un poids maximum de j.
• A chaque coordonnée dans le tableau, sélectionnez la valeur maximale que nous pouvons acquérir sans article je ou la valeur optimale que nous pouvons obtenir avec article je — celui qui est le plus grand.
• La valeur optimale disponible en se composant de l’élément i est la somme de chose je lui-même et aussi la valeur maximale qui peut être acquise avec la capacité de maintien du sac à dos.
• Effectuez cette action jusqu’à ce que vous découvriez la valeur maximale pour le O jeter.

Code

2. Problème de changement de pièces

Énoncé du problème

Supposons qu’on vous propose un tableau de nombres qui représentent la valeur de chaque pièce. À condition d’avoir une quantité spécifique, trouvez le nombre minimal de pièces nécessaires pour gagner ce montant.

Algorithme

• Initialiser un tableau de dimension n +1 , où n est la quantité. Initialiser la valeur de chaque index je dans la plage équivalente à la quantité. Cela représente la variété optimale de pièces (en utilisant des pièces de monnaie de religion 1) nécessaire pour constituer cette quantité.
• Puisqu’il n’y a pas de religion pour 0, initialisez l’instance de base où tableau = 0 .
• Pour tout autre index je nous comparons la valeur qu’il contient (qui est initialement définie sur n +1 ) avec la valeur tableau +1 où k est bien inférieur à je . Cela vérifie essentiellement l’ensemble du tableau jusqu’à i-1 pour trouver le nombre minimal possible de pièces que nous pouvons utiliser.
• Si la valeur à tout type de tableau + 1 est minime que la valeur existante à déployer modifier la valeur à déployer avec celui de tableau +1 .

Code

3. Fibonacci

Énoncé du problème

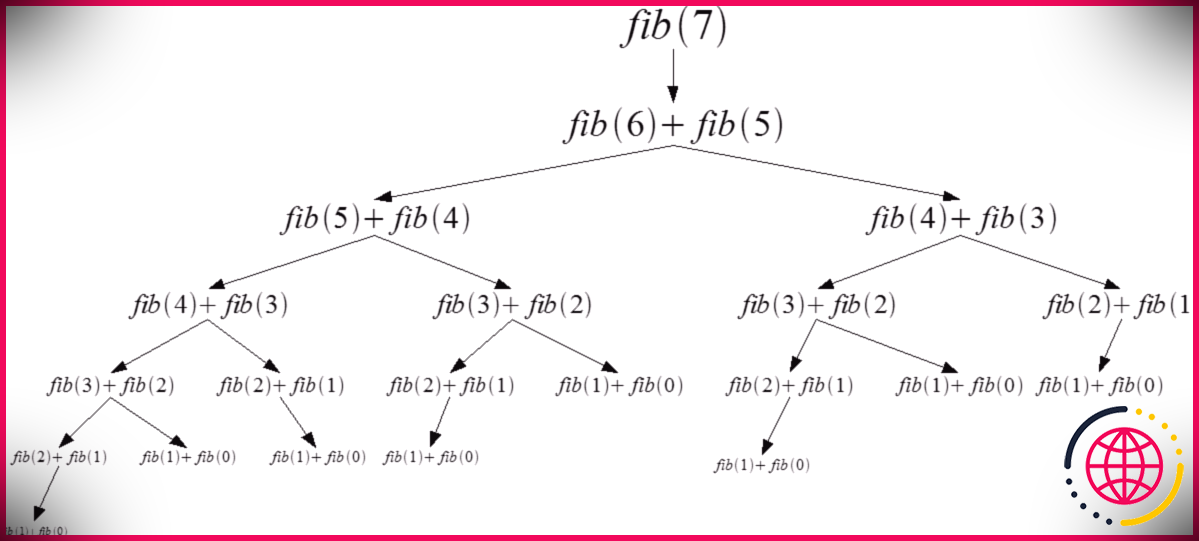
La série de Fibonacci est une séquence d’entiers où l’entier suivant dans la collection est le montant des 2 précédents.

Il est spécifié par l’adhésion à la connexion récursive : F( 0) = 0, F( n) = F( n-1) + F( n-2) où F(n) est le énième terme. Dans ce numéro, nous devons créer tous les nombres d’une série de Fibonacci jusqu’à un nième terme donné.

Algorithme

• Tout d’abord, utilisez une stratégie récursive pour effectuer la connexion de réapparition donnée.
• Résoudre récursivement ce problème implique de briser F(n) droit dans F( n-1) + F( n-2) puis en appelant la fonction avec F(n-1) et aussi F( n +2) comme critères. Nous le faisons jusqu’aux situations de base où n = 0 ou n = 1 sont arrivés à.
• Maintenant, nous utilisons une méthode appelée mémorisation. Magasinez les résultats de tous les appels de fonction dans une variété. Cela garantira certainement que pour chaque n, F(n) doit seulement être calculé dès que.
• Pour toute estimation ultérieure, sa valeur peut simplement être extraite de la plage en un temps constant.

Code

4. Sous-séquence croissante la plus longue

Énoncé du problème

Trouver la taille de la plus longue sous-séquence d’élévation à l’intérieur d’une sélection proposée. La sous-séquence d’amélioration la plus longue est une sous-séquence dans une plage de nombres avec un ordre croissant. Les nombres dans la sous-séquence doivent être uniques et en ordre croissant.

De plus, les éléments de la série n’ont pas besoin d’être successifs.

Algorithme

• Commencez par une technique récursive où vous calculez la valeur de la plus longue sous-séquence d’élévation de chaque sous-tableau possible de l’index no à l’index i, où i est inférieur ou égal à la taille de la sélection.
• Pour transformer cette approche en une approche dynamique, créez un tableau pour conserver la valeur de chaque sous-séquence. Initialisez toutes les valeurs de ce tableau à 0.
• Chaque index je de cette variété correspond à la taille de la plus longue sous-séquence rehaussante pour un sous-tableau de taille je .
• Maintenant, pour chaque appel téléphonique récursif de trouverLIS( arr, n) inspectez le n ème index de la sélection. Si cette valeur est 0, déterminez ensuite la valeur en utilisant la technique à l’étape initiale et stockez-la également à la n ème indice.
• Enfin, renvoyez la valeur maximale de la variété. Il s’agit de la longueur de la plus longue sous-séquence d’amélioration d’une dimension donnée n .

Code

Solutions aux problèmes de programmation dynamique

Maintenant que vous avez rencontré certains des problèmes de programmation dynamiques les plus populaires, il est temps d’essayer de mettre en œuvre les services par vous-même. Si vous êtes bloqué, vous pouvez toujours revenir et décrire également la section de formule pour chaque problème.

Étant donné à quel point des méthodes telles que la récursivité et des programmes dynamiques sont aujourd’hui populaires, il ne sera pas inutile de jeter un coup d’œil à certains systèmes importants où vous pouvez découvrir de telles idées et perfectionner vos capacités de codage. Bien que vous ne puissiez pas faire face à ces problèmes quotidiennement, vous les rencontrerez sans aucun doute lors d’un entretien technologique.

Naturellement, avoir la connaissance des problèmes habituels est lié à payer des récompenses lors de votre prochaine entrevue. Alors ouvrez votre IDE préféré et lancez-vous !