Un guide sur l’algorithme de la fenêtre coulissante et comment l’implémenter en Go
Effectuer des opérations sur des séquences de nombres et de caractères est un aspect crucial de la programmation. L’algorithme de la fenêtre glissante est l’un des algorithmes standard pour ce faire.
C’est une solution élégante et polyvalente qui s’est imposée dans de nombreux domaines. Cet algorithme peut jouer un rôle dans la manipulation de chaînes de caractères, la traversée de tableaux et l’optimisation des performances.
Alors, comment fonctionne l’algorithme de la fenêtre glissante, et comment pouvez-vous l’implémenter dans Go ?
Comprendre l’algorithme de la fenêtre glissante
Il existe de nombreux algorithmes supérieurs qu’il est utile de connaître en tant que programmeur, et la fenêtre glissante est l’un d’entre eux. Cet algorithme s’articule autour d’un concept simple qui consiste à maintenir une fenêtre dynamique sur une séquence de données, afin de traiter et d’analyser efficacement des sous-ensembles de ces données.
Vous pouvez appliquer cet algorithme pour résoudre des problèmes de calcul impliquant des tableaux, des chaînes ou des séquences de données.
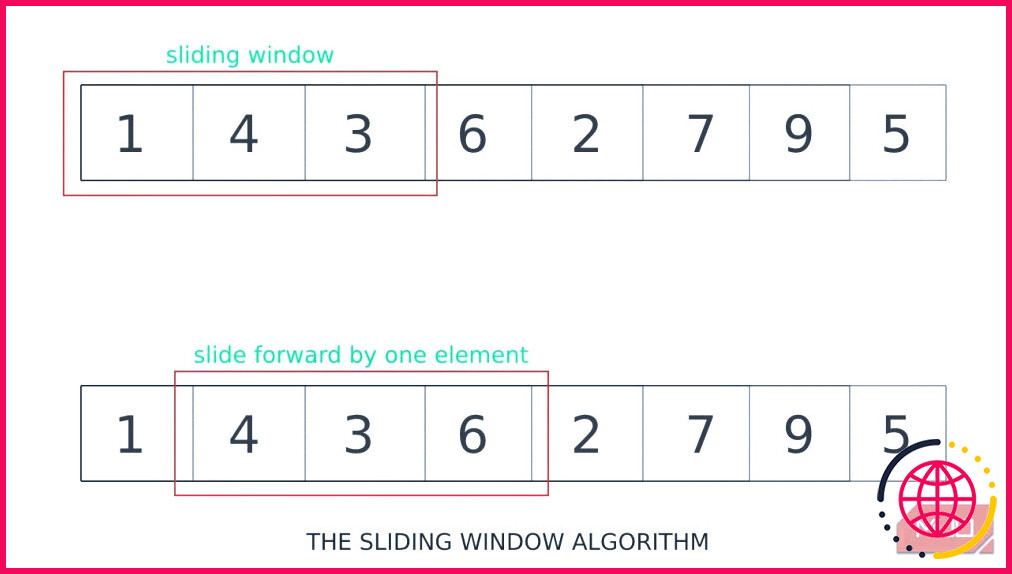
L’idée centrale de l’algorithme de la fenêtre glissante est de définir une fenêtre de taille fixe ou variable et de la déplacer dans les données d’entrée. Cela vous permet d’explorer différents sous-ensembles de l’entrée sans calculs redondants qui peuvent nuire aux performances.
Voici une représentation visuelle de son fonctionnement :
Les limites de la fenêtre peuvent être ajustées en fonction des exigences du problème spécifique.
Implémentation de l’algorithme de la fenêtre coulissante en Go
Vous pouvez utiliser un problème de codage populaire pour apprendre comment fonctionne l’algorithme de la fenêtre coulissante : trouver la plus grande somme d’un sous-réseau d’une longueur donnée.
L’objectif de cet exemple de problème est de trouver le sous-réseau de taille k dont la somme des éléments est la plus grande. La fonction de solution prend deux paramètres : le tableau d’entrée et un entier positif représentant k.
Soit le tableau d’échantillons nombres comme le montre le code ci-dessous :
Et que la longueur du sous-réseau soit k avec une valeur de 3 :
Vous pouvez alors déclarer une fonction pour trouver la somme maximale des sous-réseaux de longueur k :
Vous pensez peut-être que la fenêtre doit être un tableau qui stocke des copies des éléments cibles. C’est une option, mais ses performances sont médiocres.
Au lieu de cela, il suffit de définir les limites de la fenêtre pour en assurer le suivi. Par exemple, dans ce cas, la première fenêtre aura un indice de départ de et un indice de fin de k-1. En faisant glisser la fenêtre, vous mettrez à jour ces limites.
La première étape pour résoudre ce problème est d’obtenir la somme du premier sous-réseau de taille k. Ajoutez le code suivant à votre fonction :
Le code ci-dessus déclare les variables nécessaires à l’algorithme et trouve la somme de la première fenêtre du tableau. Il initialise ensuite maxSum avec la somme de la première fenêtre.
L’étape suivante consiste à faire glisser la fenêtre en itérant à travers les numéros à partir de l’index k jusqu’à la fin. A chaque étape du glissement de la fenêtre :
- Mise à jour somme de la fenêtre en ajoutant l’élément actuel et en soustrayant l’élément situé à windowStart.
- Mise à jour maxSum si la nouvelle valeur de windowSum est supérieure à celle-ci.
Le code suivant met en œuvre la fenêtre coulissante. Ajoutez-le à l’élément maximumSubarraySum .
À la fin de la boucle, vous aurez la plus grande somme dans maxSum que vous pouvez retourner comme résultat de la fonction :
Votre fonction complète devrait ressembler à ceci :
Vous pouvez définir une fonction principale pour tester l’algorithme, en utilisant les valeurs de nombres et k de plus tôt :
La sortie dans ce cas sera 19 qui est la somme du sous-réseau , qui est le plus grand.
Vous pouvez maintenant appliquer la même technique à des problèmes similaires, même dans d’autres langages, comme la gestion des éléments répétés dans une fenêtre à l’aide d’une carte de hachage Java, par exemple.
Des algorithmes optimaux pour des applications efficaces
Cet algorithme témoigne de la puissance des solutions efficaces lorsqu’il s’agit de résoudre des problèmes. La fenêtre coulissante maximise les performances et élimine les calculs inutiles.
Une solide compréhension de l’algorithme de la fenêtre glissante et de son implémentation en Go vous permettra d’aborder des scénarios réels lors de la création d’applications.