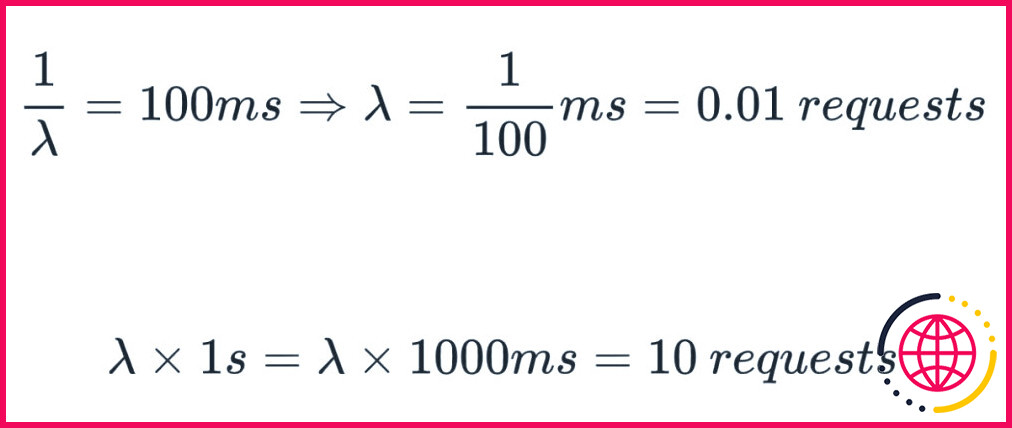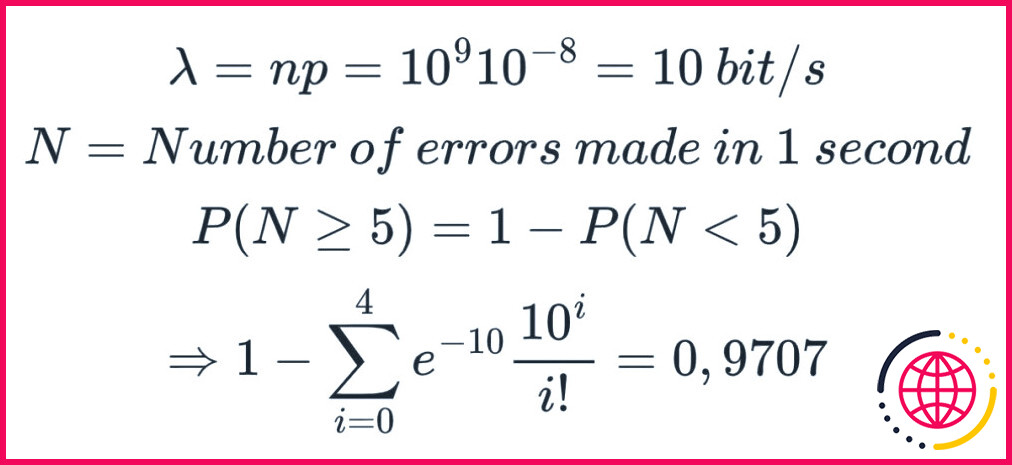Quel rôle jouent les mathématiques dans la cybersécurité ? Consultez ces exemples

Pour que la plupart des innovations soient fonctionnelles, un travail très complexe a lieu en arrière-plan. De nombreuses personnes utilisent un logiciel et ne se soucient pas de savoir pourquoi ou comment il existe. Il ne semble pas nécessaire. Dans les toutes premières années de l’informatique, les codes des appareils ainsi que les mathématiques étaient bien plus cruciaux. Cependant, si vous êtes un professionnel de la cybersécurité, les mathématiques sont toujours importantes pour vous. Pourquoi ? Quel rôle jouent les mathématiques dans la cybersécurité ?

Comment les formules mathématiques sont-elles utilisées en cybersécurité ?

Formules, formules, ainsi que des concepts intégrés au monde de l’ingénierie électrique et électronique, ainsi que des systèmes informatiques causés. Si un professionnel de la cybersécurité souhaite découvrir les systèmes informatiques et vise également une bonne profession dans ce domaine, il doit briser certaines hypothèses sur les mathématiques.

Comment le filtrage est-il utilisé ?

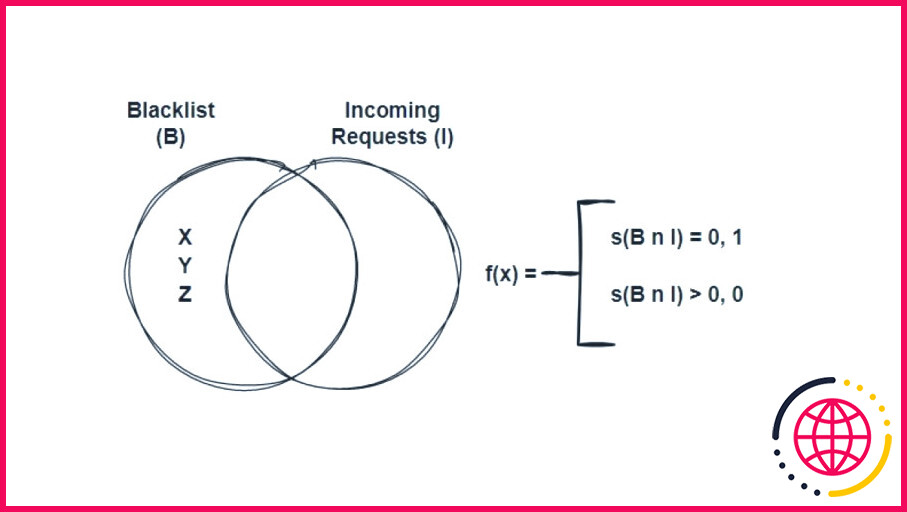
Les approches de filtrage sont activement utilisées pour différentes problématiques. Si nous examinons le problème du point de vue de la cybersécurité, il est plus fin de considérer le blacklistage comme un exemple.

Supposons que vous souhaitiez utiliser le raisonnement par liste noire pour le blocage d’IP dans un pare-feu. Pour cela, le système que vous avez l’intention de développer doit envoyer la demande entrante au mécanisme de contrôle ainsi que rechercher l’adresse IP du plan dans la liste. S’il y a une adresse IP du forfait dans cette liste, il ne permet pas le passage. La représentation mathématique de ces procédures est conforme :

Comme on peut le voir dans la représentation, si le résultat selon la méthode du f( x) est 1, la transition est activée ; sinon, elle ne l’est pas. De cette façon, vous filtrez les demandes et ne permettez le passage que des IP que vous voulez.

Quelle est la méthode de mise à l’échelle ?

Pour s’assurer de la protection d’un système, il faut d’abord qu’il soit évolutif. Pour vérifier la méthode de mise à l’échelle du point de vue de la protection, considérons un serveur internet. L’objectif est de calculer théoriquement la charge de travail sur le serveur internet.

Pour comprendre la charge de travail d’un serveur Internet, vous devez prendre en considération une préoccupation cruciale : si le temps moyen écoulé entre les demandes entrantes est de 100 ms (nanosecondes), combien de demandes sont obtenues typiquement en une seconde ?

Pour expliquer cela mathématiquement, offrons un nom à la valeur inconnue. Par exemple, laissons T soit une variable arbitraire qui représente le moment écoulé entre deux requêtes au serveur.

En guise de résultat, en mettant à l’échelle 100 ms à 1 ms vous obtenez 0,01 demande par ms de temps de dispositif. Cela suggère que vous pouvez obtenir approximativement 10 demandes sur 1000 ms.

Tirer parti de la possibilité d’erreur

Vous pouvez avoir besoin de comprendre quelle part des résultats générés par un produit de gestion des informations et des événements de sécurité (SIEM) sont des « faux positifs ». Les produits SIEM ne sont que l’un des exemples les plus faciles d’utilisation des probabilités d’erreur. Bien entendu, dans les examens d’infiltration également, vous pouvez tirer parti des possibilités d’erreur et prendre en considération un vecteur d’attaque sur la base des résultats proposés. Prenons un exemple.

La possibilité d’erreur dans la transmission de nombres binaires sur un réseau informatique fonctionnant à un milliard de bits par seconde est d’environ 10 puissance moins 8. Quelle est la probabilité de 5 erreurs ou plus en une seconde ?

Trouver ces possibilités d’erreurs et les diminuer vous donnera certainement un concept pour obtenir un système plus robuste ainsi que protégé.

Comment l’ingénierie sociale utilise le modèle de Markov

Le modèle de Markov est une modélisation statistique de la transition entre les nœuds. En d’autres termes, si vous utilisez le mode de Markov aux tweets d’un utilisateur de Twitter, vous pouvez produire un nouveau tweet à partir des mots précédemment utilisés par cet utilisateur. Il s’agit d’un modèle que de nombreux dispositifs de génération de tweets utilisent en outre. Du point de vue de la cybersécurité, les assaillants peuvent utiliser cette approche pour des frappes d’ingénierie sociale.

Par exemple, si un agresseur peut attraper les messages de la personne, il peut utiliser les messages pour produire un modèle de Markov. L’agresseur peut créer un message en fonction du résultat acquis du modèle, et la personne qui le lit peut supposer qu’il est réel. Cela est vrai pour tous les messages, comme les courriels et les médias sociaux, mais aussi pour des fichiers beaucoup plus risqués comme les relevés d’institutions financières, la correspondance principale et les documents gouvernementaux. C’est pourquoi vous devez connaître les avertissements de phishing à surveiller.

Si vous avez l’intention de voir comment la version de Markov résout une formule, vous pouvez examiner la version de codes sur GitHub.

Exemple de la théorie des jeux

Considérez le concept de jeu vidéo comme l’opposition entre la situation gagnante d’un joueur dans un jeu et la circonstance perdante de divers autres joueurs. En termes simples, pour gagner un jeu vidéo, vos adversaires doivent perdre. En outre, pour que vos challengers perdent, vous devez gagner.

Être capable d’analyser la théorie des jeux du point de vue de la cybersécurité peut vous aider à prendre la meilleure décision dans tout type de situation de dilemme. Par exemple, imaginons qu’il existe deux grandes institutions financières, ABC et XYZ.

L’institution financière ABC utilise une étape de protection spécifique pour lutter contre les risques de ransomware. L’institution financière ABC veut offrir cette étape de sécurité à la banque XYZ moyennant des frais. Est-il vraiment essentiel pour l’institution financière XYZ de recevoir des informations concernant cette étape de sécurité ?

• Coût de l’information = X
• Coût de l’absence d’information Y
• Valeur de l’information Z
• Si la banque acquiert les détails = Z– X bénéfice

Si la banque XYZ acquiert l’information et ne prend aucune mesure, elle subira certainement des pertes égales à (X+ Y ). Par conséquent, la banque XYZ peut utiliser ses informations mathématiques pour prendre la décision la plus idéale après avoir pris en compte toutes les possibilités. Vous pouvez tirer parti de nombreuses approches de la théorie des jeux vidéo, notamment pour persuader les systèmes protégés par un bureau de cybersécurité qui n’a en fait pas développé de reconnaissance mathématique et pour fournir des renseignements cybernétiques sur ces questions.

Phase de modélisation

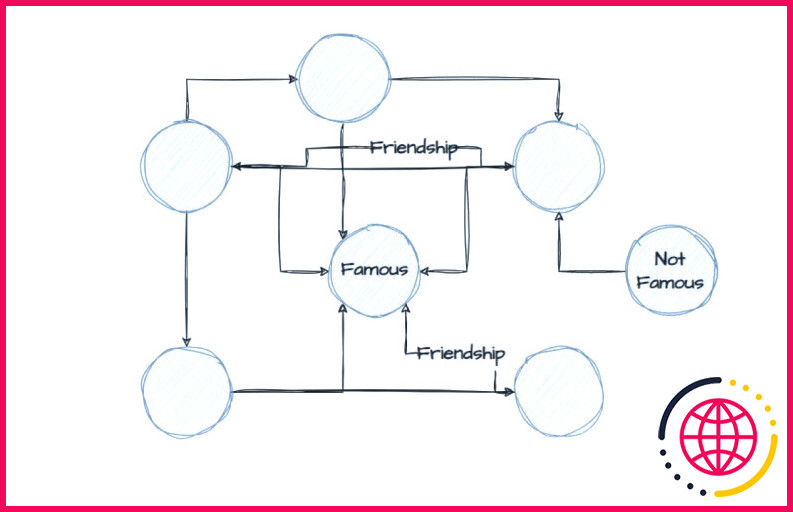
La modélisation et l’évaluation perceptible s’installent constamment. Une grande partie de la cybersécurité consiste en des étapes de collecte de connaissances et aussi d’informations. C’est pourquoi la modélisation a une valeur particulière pour l’attaque et aussi la protection. C’est là qu’intervient la théorie des graphiques, une approche fréquemment utilisée par les plateformes de réseaux sociaux comme Facebook et Twitter.

La plupart des médias sociaux de renom organisent leurs pages web, telles que les faits marquants, les histoires et les messages importants, à l’aide du concept de graphique. Voici un exemple simple de la méthode du graphique utilisée dans les sites de médias sociaux :

En résumé, la théorie des graphes est extrêmement utile pour un spécialiste de la cybersécurité afin de pouvoir analyser le trafic web du réseau et modéliser le flux du réseau.

Les mathématiques dans la cryptographie et aussi les méthodes de cryptage.

Si vous reconnaissez exactement comment les fonctionnalités fonctionnent, vous pouvez de même apprendre rapidement la cryptographie et le hachage. En termes simples, les fonctionnalités sont comme un centre de production. Vous lancez quelque chose à l’intérieur de la fonction ainsi qu’elle produit un résultat pour vous. Vous pouvez transformer la fonction, c’est-à-dire établir des règles ainsi qu’obtenir le résultat comme vous le souhaitez.

Ces fonctions sont séparées en diverses classifications entre elles. Cependant, comme il est important que vous ayez un mot de passe solide et incassable, nous ne couvrirons que les fonctions unidirectionnelles. Si vous considérez les fonctions à sens unique selon l’instance de l’installation de production, ce sont des fonctions qui ne peuvent pas récupérer le résultat qu’elles produisent. Ainsi, vous obtiendrez certainement un résultat, mais ce résultat restera tel quel. Il n’y a pas de conception inverse.

Le meilleur endroit pour utiliser cela est très certainement dans le cryptage. C’est ainsi que les fonctions de hachage fonctionnent, par exemple. Si vous passez un texte avec la fonction de hachage, elle vous offrira une valeur complètement différente. Cette valeur n’est plus réversible, vous pouvez donc cacher et sécuriser votre texte.

Ai-je vraiment besoin de connaître les mathématiques ?

Si vous vous occupez de vulnérabilités dans des milliers de documents et aussi des dizaines de centaines de lignes de code ; un site qui a des milliers de centaines de visiteurs ; ou une application bancaire où les individus paient leurs frais .vous devrez peut-être faire appel aux mathématiques. Sinon, vous ne pourrez pas mener à bien votre travail. Cependant une compréhension profonde des mathématiques vous place une action en avance.

Abonnez-vous à notre e-newsletter