Comment utiliser un diagramme de dispersion dans Microsoft Excel pour prédire le comportement des données.

Une évaluation efficace des données nécessite une compréhension claire du partenariat entre les variables et les quantités impliquées. Aussi bien que si vous avez de grandes informations, vous pouvez même les utiliser pour prévoir le comportement des données.

Cependant, à moins d’être un mathématicien, il est impossible de développer une formule à partir d’un ensemble de données. Pourtant, avec Microsoft Excel, pratiquement tout le monde peut le faire en utilisant un diagramme de dispersion. Voici comment.

Créer un graphique en nuage de points dans Microsoft Excel

Avant de pouvoir commencer à prédire un modèle, vous devez d’abord produire un graphique en nuage de points pour en trouver un. L’histoire en nuage de points fournit la relation en entre 2 variables le long des deux axes du graphique, avec une variable indépendante et l’autre dépendante.

La variable indépendante est généralement représentée sur l’axe horizontal du graphique, tandis que vous pouvez trouver la variable dépendante sur son axe vertical. La relation entre les deux est représentée par la ligne du graphique.

Pour produire un graphique en nuage de points sur une feuille Excel, respectez les étapes énumérées ci-dessous :

1. Ouvrez la feuille de calcul comportant les données que vous souhaitez tracer sur le graphique en nuage de points.
2. Placez la variable indépendante dans la colonne de gauche et la variable dépendante dans la colonne de droite.
3. Sélectionnez la valeur des deux colonnes que vous souhaitez tracer.
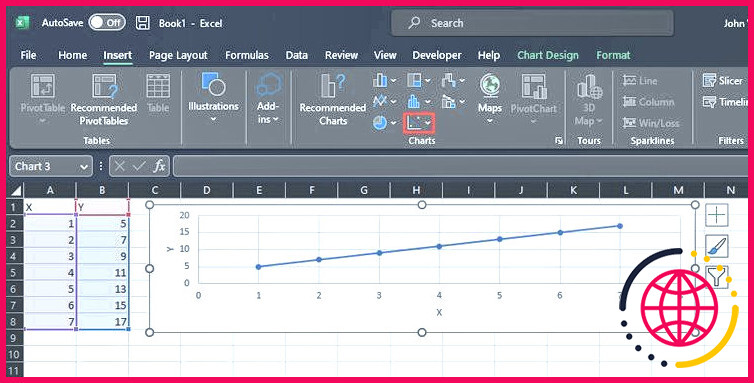
4. Cliquez sur le bouton Insérer ainsi que sur l’onglet Graphiques groupe. Actuellement, cliquez sur Insérer un graphique de dispersion( X, Y) ou un graphique à bulles.
5. Ici, vous trouverez certainement différents styles de diagramme de dispersion. Sélectionnez parmi eux en cliquant dessus.
6. Cela va certainement présenter le graphique sur l’écran. Changez le nom des axes ainsi que le titre du graphique.

Dessiner une ligne de tendance sur un graphique en nuage de points.

Afin de présenter la connexion entre les variables du graphique, une ligne de tendance est appelée. La ligne de tendance doit ressembler ou se chevaucher avec les valeurs d’information sur le graphique afin d’approximer précisément la relation entre les variables. Pour attirer une ligne de tendance sur le graphique en nuage de points :

1. Faites un clic droit sur n’importe quel point de données sur le graphique en nuage de points.
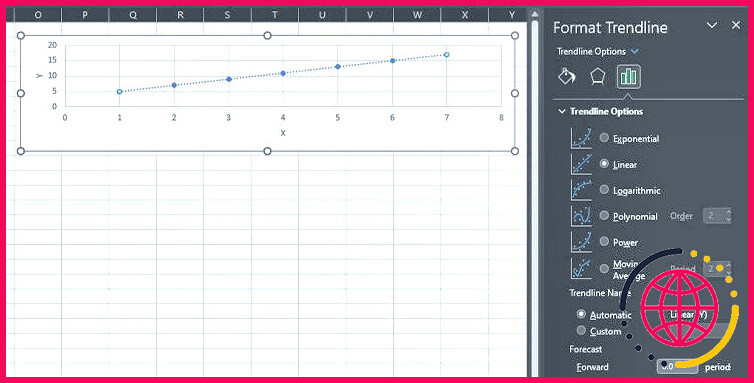
2. Dans la liste des alternatives qui s’affichent, sélectionnez . Ajouter une ligne de tendance.
3. A Format de la ligne de tendance s’affichera certainement sur le côté droit avec l’option Linéaire sélectionné par défaut.

Ceci ajoutera une ligne de tendance (ligne droite peuplée) à votre graphique en nuage de points.

Options de formatage de la ligne de tendance pour ajuster la courbe des valeurs des données.

Nous voulons ajuster le contour de la ligne de tendance aussi près du tracé de contour que possible. En faisant cela, nous pouvons obtenir une compréhension directe de la relation approximative entre les variables. Pour ce faire, adhérez aux étapes ci-dessous :

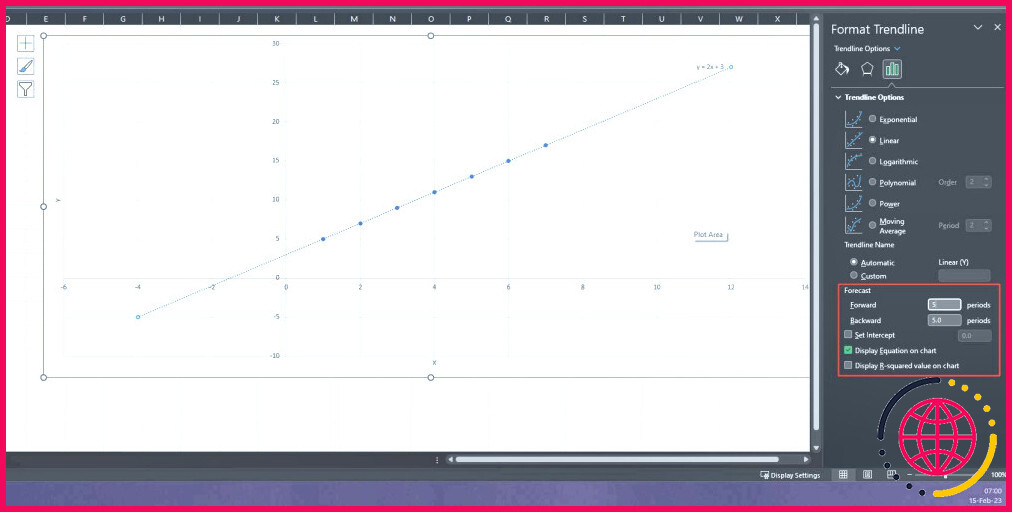
1. Choisissez différents contours parmi OPTIONS DE LIGNE DE TENDANCE dans le Format de la ligne de tendance pour ajuster en courbe la ligne de tendance avec une histoire de contour.
2. Cochez la Afficher l’équation sur le graphique pour présenter la courbe en équation de forme sur le graphique en nuage de points.

Prévision des valeurs en avant et en arrière en fonction des tendances.

Après l’ajustement des contours, vous pouvez utiliser cette ligne de tendance pour anticiper les valeurs précédentes et aussi futures qui ne font pas partie de cet ensemble de données. Vous pouvez accomplir cela en désignant une valeur sous la section Prévision de la fenêtre Format Trendline. Incluez vos durées souhaitées sous la section Prévision et En arrière alternatives pour observer les valeurs attendues sur le diagramme de dispersion.

Prévoir la relation entre plusieurs variables indépendantes et dépendantes pour formuler une équation.

Les données ont parfois plusieurs variables indépendantes qui produisent des valeurs résultantes. Dans de tels cas, le schéma peut ne pas être simple. Pour identifier la connexion, vous pouvez avoir à rechercher des tendances parmi la quantité dépendante ainsi que les variables indépendantes individuelles.

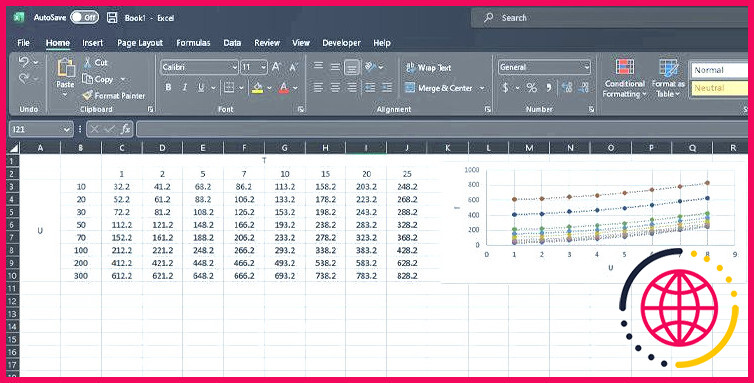
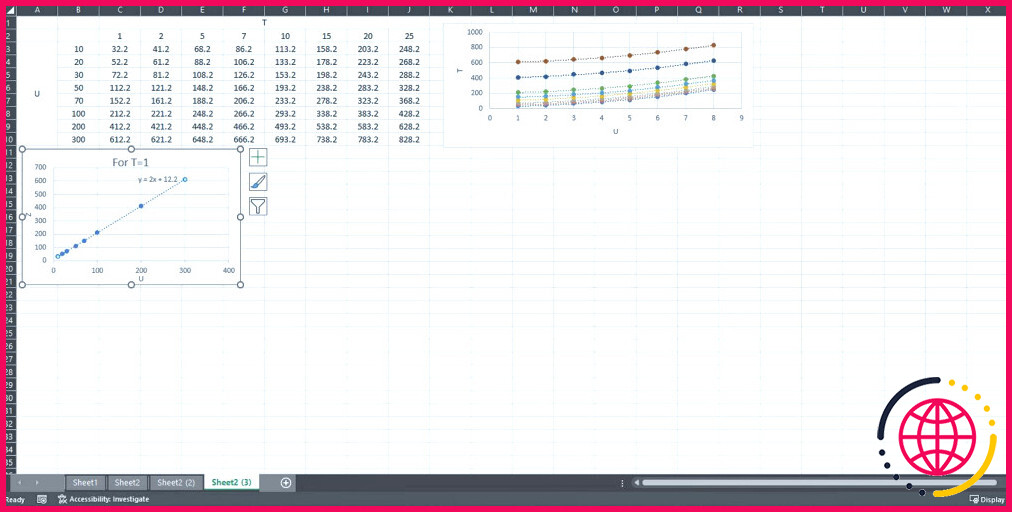
Dans la figure listée ci-dessous, nous avons un ensemble d’informations qui contient 2 variables indépendantes. Dans le graphique, l’axe droit représente la variable. u et l’axe vertical représente la variable dépendante résultante. Chaque ligne du graphique est également une fonction de la variable T.

Ici, nous allons certainement trouver une méthode pour localiser la relation approximative entre la variable dépendante Y( U, T) (ou valeur résultante) et aussi les variables indépendantes U et T. Cela nous permettrait de théoriser ces valeurs variables pour prévoir le comportement des données.

Pour ce faire, adhérez aux étapes ci-dessous :

1. D’abord, nous allons certainement localiser le partenariat entre une variable indépendante (U ) et aussi la résultante dépendante Y. Conserver la valeur de diverses autres valeurs indépendantes (T ) cohérente en ne choisissant qu’une seule colonne à chaque fois.
2. Sélectionnez les cellules B 3 à B 10 pour choisir U ainsi que les cellules C 3 à C 10 (valeur résultante à T= 1) ainsi que l’utilisation d’un diagramme de dispersion pour les mettre en évidence.
3. Tracez maintenant la ligne de fuite et utilisez la ligne de meilleur ajustement affichée dans le diagramme de dispersion. Format de la ligne de tendance fenêtre d’accueil qui correspond à l’ensemble des informations. Dans ce cas, nous avons observé que la ligne de tendance « droite » correspond le mieux à la courbe.
4. Cliquez sur Afficher la formule sur le graphique dans le Format de la ligne de tendance fenêtre d’accueil de la ligne.
5. Renommez les axes du graphique en fonction des variables de données.
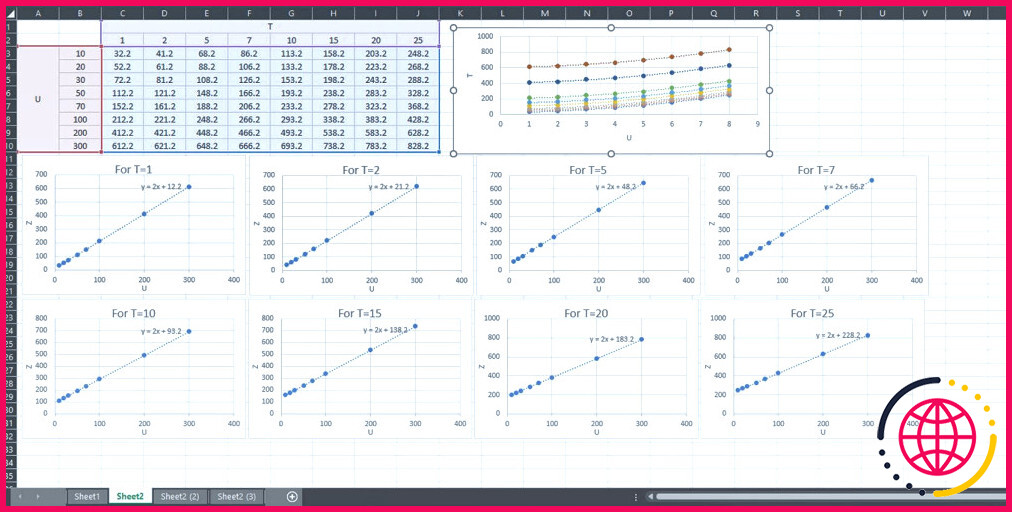
6. Ensuite, vous devez développer un diagramme de dispersion pour toutes les diverses autres variables sous T. Suivez les étapes un à cinq, mais sélectionnez les colonnes D 3 pour D 10 (T= 2), E 3 à E 10 (T= 5), F 3 à F 10 (T= 7), G 3 à G 10 (T= 10), H 3 à H 10 (T= 15), I 3 à I 10 (T= 20) et J 3 à J 10 (T= 20) individuellement avec la variable U y compris les cellules B 3 à B 10.
7. Vous devriez découvrir les formules conformes présentées sur les graphiques.
   

   T

   Y

   T= 1	Y= 2U +12.2
   T= 2	Y= 2U +21.2
   T= 5	Y= 2U +48.2
   T= 7	Y= 2U +66.2
   T= 10	Y= 2U +93.2
   T= 15	Y= 2U +138.2
   T= 20	Y= 2U +183.2
   T= 25	Y= 2U +228.2

   Nous pouvons observer que toutes les équations sont droites et ont exactement le même coefficient sur la variable U. Cela nous rapproche du verdict selon lequel Y est égal à 2U et aussi d’autres valeurs différentes qui peuvent être une fonction de la variable T.

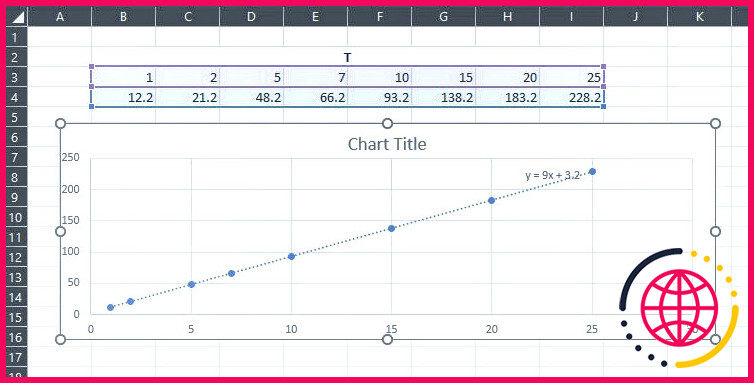
8. Notez ces valeurs indépendamment les unes des autres et disposez-les comme indiqué ci-dessous (chaque valeur avec sa valeur variable notée, par exemple 12.2 avec T= 1 et 228 avec T= 25 etc). Tracez maintenant un diagramme de dispersion de ces valeurs et montrez la formule qui établit le lien entre ces valeurs et la variable T.
9. Enfin, nous pouvons relier Y( U, T) comme

Vous pouvez confirmer ces valeurs en traçant cette formule pour différentes valeurs de U et aussi T. De même, vous pouvez prévoir le comportement de Y( U, T) pour différentes valeurs des variables U ainsi que T non disponibles avec cette collecte de données.

Il n’est pas nécessaire d’être un expert en mathématiques pour prédire les tendances dans Microsoft Excel.

Maintenant que vous reconnaissez juste comment localiser la relation entre une fonction et aussi ses conditions dépendantes, vous pouvez tirer des conclusions légitimes sur les actions de la fonction. Offert que vous avez toutes les variables nécessaires qui affectent la fonction mathématique, vous pouvez prédire avec précision sa valeur dans les conditions offertes.

Microsoft Excel est un dispositif fantastique qui vous permet d’esquisser des fonctions multivariables également. Maintenant que vous avez vos informations, vous devez en plus explorer les différentes méthodes que vous pouvez créer des graphiques efficaces ainsi que des diagrammes pour les offrir.

Abonnez-vous à notre bulletin d’information